Physics of a Ground Pass One of the most fundamental elements of a soccer player's repertoire is a simple ground pass. Even though this may not seem like such an intriguing aspect of the game, the physics behind this concept is crucial. source: http://www.soccer-training-info.com/soccer_passing_skills.asp Rolling Motion Rolling motion can be described as a combination of both translational and rotational motion. The center of mass of the ball will move with translational motion, while the rest of the ball will rotate about the center of mass. 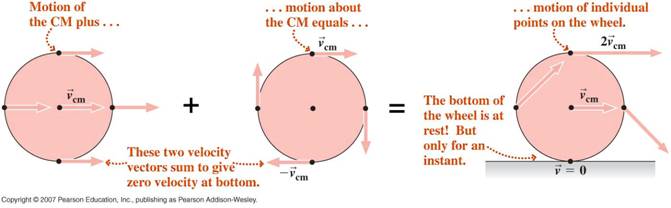source: http://www.physics.louisville.edu/cldavis/phys298/notes/tranrot_comb.html The image above does an excellent job of depicting how rolling motion is truly a combination of both the translational motion of the center of mass and the rotational motion of the rest of object around that center of mass. Lets first take a look at the velocity of the center of mass. If the ball makes one complete rotation, the the distance the ball has traveled is equal to the circumference, 2$pi$R. We can in turn find the velocity of the center of mass by using the equation, xf-xi=vcm(tf-ti). So by knowing the distance traveled, the equation becomes 2piR=vcm(tf-ti). But we know that the time it takes for an object to travel one complete rotation is T (the period). Substituting this into the equation and solving for vcm gives: vcm=(2piR)/T. But (2pi)/T is the same as the angular velocity, w. Now we can see the the velocity of the center of mass is: vcm=Rw, where R is the radius of the ball and w is the angular velocity. Now lets take a look at the velocity of the very top of the ball, and at the very bottom of the ball. First, the velocity at any point, p, on the ball can be written as: vp=vcm+vp, rel. Taking this into account, for the very top of the ball, the velocity relative to the center of mass is Rw. This is the same velocity that the center of mass has, so the velocity at the top of the ball is 2vcm, or 2Rw. Finally, lets take a look at the velocity at the very bottom of the ball, the point that is touching the ground, assuming there is no slipping. Using the same principles that we did with the top of the ball, the velocity relative to the center of mass at the bottom of the ball is -Rw, because relative to the center of mass, it is moving in the negative direction. When adding this value to the velocity of the center of mass, we get that the velocity at the bottom of the ball is 0. This means that for any object that is experiencing rolling motion, without any slipping, the point that is touching the ground is instantaneously at rest! source: http://www.wallcoo.net/sport/ball/html/wallpaper18.html