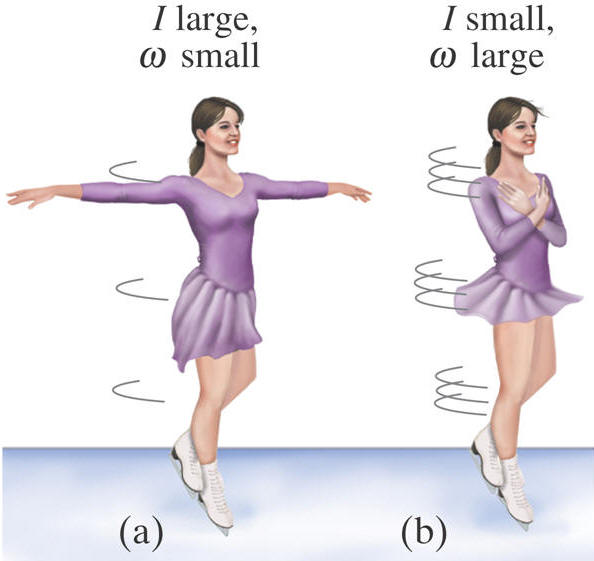
To
keep
angular
momentum
from getting too complicated, we will think of the figure skater
as a simple rigid body. Through figure skating, the concept of
angular momentum can be best described by what we see happen
when a skater is spinning slowly with her arms and legs out wide
and then as soon as she pulls her arms in, the speed of her
spinning increases significantly. This is a good example of the
law of conservation of momentum. From Randall Knight’s Physics
for Scientists and Engineers textbook, the conservation of
angular momentum is explained as follows: “The angular momentum
L of an isolated system (net Torque = 0) is conserved. The final
angular momentum Lf is equal to the initial angular momentum Li.
Both the magnitude and direction of L are unchanged.” Another
idea to note is the equation for angular momentum: L=Iω
(angular momentum = moment of inertia x angular velocity). With
these facts in mind, lets think about what is happening when a
skater is spinning. When a skaters arms and legs are
outstretched, her moment of inertia has a large magnitude and
her angular velocity has a small magnitude. If she starts
pulling in her arms, we can visibly see that her angular
velocity has increased and thus we can deduce that in order to
satisfy the law of conservation of angular momentum her moment
of inertia has decreased.
