|
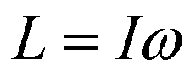 |
The equation for Angular
Momentum resides on the left. We can see that the only item in the
equation that we can very is the omega (the odd looking "w"), which if
you remember is the angular velocity (the spin) given to the disk. |
| Now, why do we care about
the angular momentum? Well, with the momentum gained from the
angular velocity the disc will resist any angular movement and try
to continue on the path which it was launched. Now you might ask
where do these crazy angular movements come from? Well remember
that the center of lift is forward of the center of mass. Because
of this there will be moments acting on the system. |
| Moments? Well you can
think of a rusty bolt and a crescent wrench. The longer the lever
arm acting on the bolt, the more force you can put on it. Now try
to apply this line of thinking to the center of mass of the Frisbee and
the center of lift, along with the angular velocity. Now there are
all kinds of lever arms! |
| Now lets pick a coordinate
system we can use. We will use a system where the Z axis comes
straight out of the center of mass, pointing up. The X and Y axis
will be on the surface of the disk. None of the axes will rotate
along with the disk. The sums of the moments corresponding to
their respective axes are shown to the right. These are by
definition. (5) We will not go into solving these
equations here, but I will say that we would take the time derivative of
the moment about the Z axis with respect to time would be zero due to
the coordinate system we have chosen. |
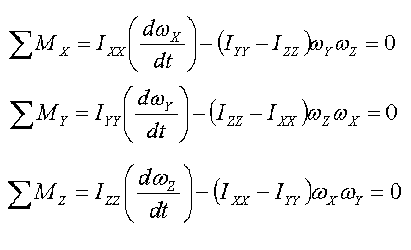 |
|
