
|
Lift |
| Typically a disc is designed with the Center of Lift (CP) just forward for the Center of Mass. The reason behind this is to give the disc a natural angle of attack, or tilt, into the air flow. |
|
|
A down side to this design is that the disc
experiences an unstable pitching motion to either side. This can
easily be seen if you toss a Frisbee without any spin. The disc will
pitch to one side or another.
|
| As the air flow travels across the surface of the disc, many interesting things happen to it. One of these being the Kutta Condition. This condition states that a fluid ( in this case air) will tend to travel along the contour of a curved surface. This effect actually contributes to the lift force. |
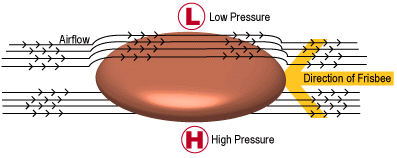
| It is important here to discuss
something called the Bernoulli Effect. Simply stated, areas of high
velocity (speed) over a surface in a fluid experiences a low pressure area,
where as an area of low velocity experiences high pressure. The
Frisbee can be generalized as an airplane wing. Air flow over the top
of the disc travels at a higher velocity than the lower flow, so an area of
low pressure is created, so the disc rises. (Note: This is a very generalized explanation) (6) |
 |
| As descent as this explanation
is, it is not entirely correct. The Bernoulli Effect, which works
great in general, disregards the vorticity of a fluid. In a best case
scenario we can use it as an approximation. There is also another component which aids in the lift force, but this will be covered later.
|
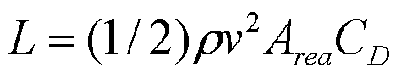 |
To the left is the equation for Lift. The "little p" stands for density, v is for velocity, A is the area, and C is the drag coefficient. (5) |