source: www.math.armstrong.edu/mmacalc/gallery/flow.gif
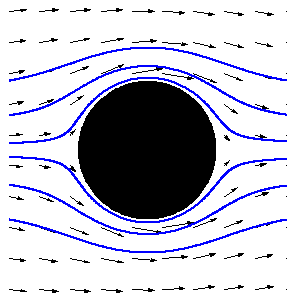
Stokes Flow- a stationary sphere in a uniform flow
Analytic solutions exist for the flow about a sphere for Reynolds numbers(Re) much less than 1. The Reynolds number is an indicator of various fluid properties and is defined as:
Re=UL/u
Where U is a velocity representative of the flow, L is a length
representative of the flow, and u is the
kinematic viscosity.
So for small Reynolds numbers the fluid velocities will be small, the
sphere will be small, and the viscosity will be large.
Using the Navier-Stokes equation and the continuity equation to
describe the fluid motions, with the assumption that their is a
"creeping flow" (which is often the case for very small Re) then a
solution is known and was discovered by Stokes in the 19th
Century. The boundary conditions used for the solution are
standard, no slip conditions at the sphere surface (fluid velocities
go to zero) and also that the flow must be uniform an infinite
distance from the sphere. Under all these conditions, the
solution looks something like the figure below, where the arrows
represent the velocity field and the blue lines are streamlines.

source:
www.math.armstrong.edu/mmacalc/gallery/flow.gif