|
|
[ http://www.britannica.com/bcom/art/00118/83.jpg ]
|
|
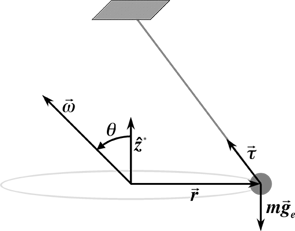
Armed with the knowledge of fictitious forces and their mathematical formalisms, we are ready to investigate the Foucault pendulum. To begin our analysis, a little introduction is required. The pendulum in question consist of a long rod and fairly massive bob. The ones that demonstrate the desired effect most suitably are equipped with a device to give them a small consistent push, to compensate for the attrition of energy due to friction. Once set in motion with a regular period, the pendulum's plane of swing will precess. This is usually not apparent unless viewed with time lapse photography or by taking measurements over the course of a day, as the rate of precession is related to latitude, but limited to the rate of rotation of the Earth. Seen from the frame of reference of the earthly observer, an unkown force is at work, the source of which cannot be found. [1], [2]
Derivation [3]
From the previous pages it should be clear that the culprit is the Coriolis force; that in fact, the pendulum is obeying the conservation of linear momentum, and the Earth is turning beneath it.
We should begin by first assuming that the pendulum will precess. The formulation of this assumption was obtained through the observation mentioned above.
To find the rate of precess, we should examine
Newton's second law, adapted for the pendulum.
(F1)
The tension in the rod is the external force.
The primed derivatives represent the coordinate
system with respect to the Earth. In order to find the precession of
the pendulum in that Earth's coordinate system, caused by the
Coriolis force, yet another rotating coordinate system is used.
(F2), where 
is the angular velocity about 
.
This is the quantity in question, since
refers to the radial vector extending from the Earth, which is in
plane of the pendulums swing.
The starred derivatives are representative of the coordinate system that is precessing with the pendulum. Note that the starred coordinate system is embedded in the Earth's coordinate system, which from this point of view, makes the Earth's rotation imperceptable.
Taking the second derivative so that we may
integrate the second system (starred), into the primed system we have
the equation:
(F3)
Now combining equations (F1)
and (F4):
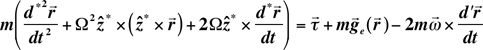(F5)
Substituting in (F2)
for the primed velocity:
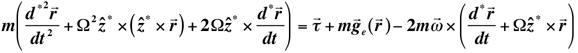(F6)
Now multiply through by the mass:
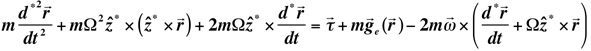(F7)
Distributing the cross product:
(F8)
Solving for the starred force, we arrive at:
(F9)
With the following vector identity we may
represent (F10)
in a more useful form:
(F11)
Applying the identity to each triple cross
product
(F12)
(F13)
Replacing each triple cross product with it's dot
product form:
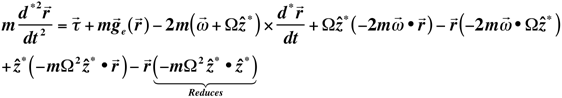(F14)
This can be reduced to the following:
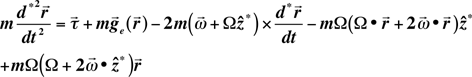(F15)
The above equation describes the forces acting on
the pendulum within the reference frame of the precessing pendulum.
Thus, the rotation of the Earth and the precession of the pendulum
will be imperceptible. By experimentation we know that the pendulum
will not move out of the 
plane.
All of the terms in the expression above lie in
the
plane except the 
term.
To insure that is will indeed find its way into
the
plane we induce a condition of orthogonality, setting the 
equal to zero. This insures that the above cross product will lie in
the desired plane. This also allows us to solve for .
Starting with the dot product equal to zero:
(F16)
Distributing the dot product:
(F17)
We end up with the following dot product form:
(F18)
Moving the dot product term:
(F19)
Using the definition of a dot product we may solve
for :
(F20),
where 
is the angle between 
and
or rather the angle between the pendulum's central/rotation axis and
the Earth's rotational axis.
We arrive at the precession of a pendulum on Earth, or for that matter, any rotating body.
In finality, we have cracked this problem open like a stale fortune cookie; and what's more, the magic eight ball says it's true.
Q.E.D., and remember kids, don't try this at home.
References
[1] http://www.eb.com:180/bol/topic?eu=35650&sctn=1
[2] http://www.eb.com:180/bol/topic?eu=35652&sctn=1
[3] Mechanics: Third Edition, by Kieth
R. Symon, pages 281 - 284
(F4)
(F10)