[ Created by Everett Travis ]
[ Diagram inspired by Keith R. Symon (Mechanics: Third Edition, page 281) ]

When multiplied by mass, the effective force in the rotating system is this:
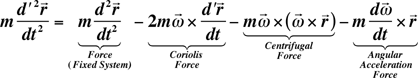(C1)

This deserves some explanation. Some of it is, after all, what this web page is about. or is the inertial force, and the rest are fictitious forces. When I say fictitious, I mean that their effect is real, you would feel them, but they aren't caused by anything other than the fact that the coordinate system is rotating, there are no invisible undetectable agents of evil at work here. Yet you do feel them, and that is what makes them interesting, and relevant to this web page.

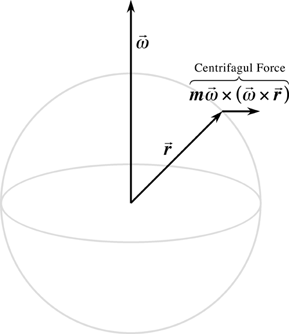
The first fictitious term is the one of the most relevance. It is known as the Coriolis force, but we won't go any further with it until the others have had some explanation. The second term, the triple cross product, is the centrifugal force. You are probably thinking that there really is no such thing as centrifugal force, just the centripetal acceleration necessary to deviate an object's motion in a circular path. You are correct, it is just another result of a moving coordinate system. To clarify the direction of acceleration, consider the vector direction of to be the direction that a screw would move if you rotated it with a screw driver, and to be a vector pointing radially out of the earth. Remembering the right hand rule, points into the plane of your mental chalkboard (if you have drawn the earth in cross section on that chalkboard). With this in mind, points into the Earth. Notice, that the component of perpendicular to the surface of the Earth varies in magnitude depending on where you stand: it is equal to zero at the poles, and maximum at the equator. So subtracting this from the mass based gravitational force gives you the effective gravity at your location. This is incidentally why the Earth is not a sphere, but an oblate spheroid, bulging at the equator. It is also why NASA launches more missions from Cape Canaveral, Florida instead of Barrow, Alaska. The last term exclusively deals with a system in which the rate of angular velocity changes. In further calculations, we dismiss this since it does not apply to the Earth. [1], [2]

This being said, lets move on to the Coriolis force.

The term is known as the Coriolis force. This force is not in actuality a real force, but the result of the law of inertia in a rotating coordinate system. Any object in constant uniform motion will remain in constant uniform motion unless acted on by an outside force. For the purposes of explanation, it is helpful to imagine a rotating system, such as the surface of the Earth, where an object has been released into a uniform motion. Imagine this object moving in a north to south direction at an appreciable speed. Since there are no external forces, but the rotating system is turning while the object is in motion, the object will appear to curve in its motion to an observer moving with the system. Of course, if an observer attempts to oppose this perceived curving motion, he will have to exert a force, and by Newton's third law, he will feel an oppositely directed force. This is the Coriolis force. [2]

Click here to see the Coriolis force in action.

References
[1] http://www.eb.com:180/bol/topic?eu=119063&sctn=5
[2] Mechanics: Third Edition, by Kieth R. Symon, pages 279 & 280