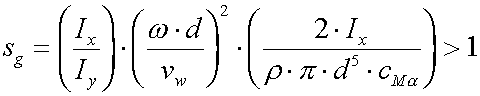
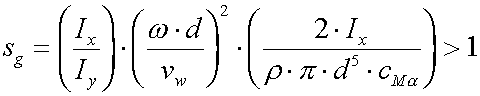
|
|
Overturning moment coefficient derivative; cMa(B,Ma) |
|
|
Gyroscopic stability factor |
It can be shown by a mathematical treatment that this condition is fulfilled, if the gyroscopic stability factor sg exceeds unity. This demand is called the gyroscopic stability condition. A bullet can be made gyroscopically stable by sufficiently spinning it (by increasing w!).
As the spin rate w decreases more
slowly than the velocity vw, the gyroscopic stability
factor sg, at least close to the muzzle, continuously
increases. An practical example is shown in a figure ![]() .
.
Thus, if a bullet is gyroscopically stable at the muzzle, it will be
gyroscopically stable for the rest of its flight. The quantity sg
also depends on the air density r and this is
the reason, why special attention has to be paid to guarantee gyroscopic
stability at extreme cold weather conditions.
Bullet and gun designers usually prefer sg > 1.2...1.5, but it is also possible to introduce too much stabilization. This is called over-stabilization.
The gyroscopic (also called static) stability factor depends on only one aerodynamic coefficient (the overturning moment coefficient derivative cMa) and thus is much easier to determine than the dynamic stability factor. This may be the reason, why some ballistic publications only consider static stability if it comes to stability considerations.
However, the gyroscopic stability condition only is a necessary condition to guarantee a stable flight, but is by no means sufficient. Two other conditions - the conditions of dynamic stability and the tractability condition must be fulfilled.