The centrifugal force

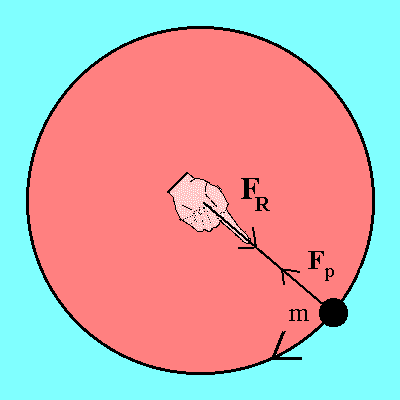
Let us consider a mass on a string swinging around in a circle (e.g. in vacuum, with constant speed). This mass experiences the centripetal force F_p, which applies at the center of mass of the body and is directed inward, towards the center of the circle.
However the hand, holding the string "feels" an outward directed force - according to Newton´s third law (actio=reactio). This "reactive" force F_R has the same magnitude as the centripetal force - but opposite direction - and applies at the hand holding the string. This reactive force is not the centrifugal force, because the centrifugal force applies at the center of mass of the body.

The necessity to consider a centrifugal force can best be understood from the following:
Assume a mass on a spring that swings around in a circle with constant velocity. This spring will show some tension.
From the position of an observer in a reference system which rotates with the mass one finds:

the mass does not move,
there is a tension in the spring

This tension could only be explained by the existence of an outward directed force - the centrifugal force.

The necessity to consider the centrifugal force simply arises from the fact, that the reference system fixed to the earth, within which we consider bullet motion is rotating. Newton´s second law only applies in an "inertial" reference system, which is a reference system which either rests or which moves with constant linear speed. Obviously, the rotating earth is not an inertial system. The centrifugal force - as well as the coriolis force - must be considered as additional "fictious" forces to apply Newtons second law

Total force = mass * acceleration

even in a reference system, which is fixed to the rotating earth.