A linear polarizer removes the electric field orthogonal to the axis of polarization

Linear Filters

There are two general categories of linear polarizers: Absorptive and Beam-Splitting. An easy conceptual filter is a fine wire-grid. The component of the electric field parallel to the wires induces a current in the wires, which cancels the field. The component orthogonal to the wires doesn't induce a current, so the field remains unchanged. This means, for light polarized with angle θ relative to the axis of the polarizer, the electric field of the resultant light is E₀cosθ. Since intensity is proportional to E², I=I₀cos²θ. This is known as Malus' law. This property can be used to regulate the intensity of the light from a constant polarized source.

Light from most sources, like the sun and lightbulbs, are unpolarized. This means not that each photon is unpolarized, but that the polarization of each photon is random, which means that the light as a whole has no polarization. After passing through a linear filter, the intensity of the light is halved. This is because the average value of cos²θ is 1/2.

One problem is that with only one filter it is impossible to twist the polarization by 90˚ (because cos(π/2)=0.) However, with a series of filters, it is possible to twist the polarization by 90˚. With two filters, the light retains 1/4 of its intensity. The maximum intensity of light twisted 90˚ by n filters is:

For example, with 5 filters, the maximum intensity is .605I₀; with 20 filters the maximum intensity is .884I₀. Actual filters do not achieve the theoretical throughput of the ideal filter though, so the actual intensity is less.^[2]

Circularly Polarized light

Circular Filters

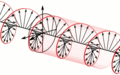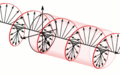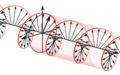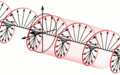
The speed of light varies by the refractive index of a material; for example the speed of light is 200,000 km/s through glass as opposed to 300,000 km/s in a vacuum. Some materials have different refractive indecies for horizontal and vertical polarization. If polarized light is shone on the material, the horizontal and vertical components will be out of phase on the other side. By cutting the material to the correct width, the phase shift between the axes is such that the electric field will vary in a helical pattern. This can produce either counter-clockwise or clockwise circularly polarized light. These are called quarter-wave plates.^[3]

The angle which the liquid crystals (LCs) turn to determines the brightness of the pixel

LCDs

If you look closely at your screen, you should notice that the picture is a large array of colored squares arranged in a grid. Each square, or 'pixel', has its own distinct color. This color is the combination of red, green, and blue light each in various intensities. These primary colors can reproduce any color which the human eye can see, because our eyes are trichromatic. In other words, they approximate specific wavelengths of light by analyzing the intensity of each of three color channels. Displays make use of this shortcoming by only displaying three wavelengths which selectively target each type of receptor.

Various arrangements of subpixels

Liquid Crystal Displays (LCDs) have a backlight which evenly illuminates the entirety of the screen. In each pixel, there are three 'subpixels' which tint the backlight red, green, or blue. To vary the intensity of each subpixel, the LCD first polarizes the light before being tinted by the subpixel. After the tinting, there is a Liquid Crystal (LC) layer followed by a polarization filter orthogonal to the first filter. With the LC turned off, no light passes through because the back and front filters are turned 90˚ from each other.

The Liquid Crystal part of the LCD is the part which makes them work. A layer of LC acts as a polarized filter. Each successive layer of LC aligns itself with the previous, so in the absence of an outside force LC acts just as a regular linear filter. In the presence of a voltage, the top layer will align itself with the voltage and twist the column of LC below it. This acts as a series of linear polarized filters, and reorient the angle of polarization of the light with very little loss. Varying the voltage will vary the final angle of polarization before the light hits the front filter, which determines the intensity of the light for each subpixel. ^[1]

The right image cuts down on glare by using a polarized filter

Photography

Light can become polarized when it reflects off of a non-metalic surface. Dielectrics (most non-metals) reflect or transmit light in different quantities based on its polarization and angle of incidence. Since the main source of illumination outside is from the sun, much of the reflected light is going to be polarized the same way. Photographers can create better pictures by adding a polarizing filter to the camera lens to adjust the amount of glare in a scene.

This is also taken advantage of by polarized sunglasses which can cut down on glare from roads and water. In some situations you can see quite deeply into water due to the lack of reflected sunlight. ^[4]

3D Movies

Stereopsis lets your brain fake 3D by analyzing the differences between two images

Amazingly enough, humans don't see in three dimensions; our eyes can only see 2-D images. However, our brain can figure out how far away objects are by analyzing the differences in what each eye sees. This process is known as Stereopsis. Without two eyes, you are not able to see depth.

Crowd watching an anaglyph 3D movie

Because our brain can only see pseudo-3D, movie makers can hijack this process to create the illusion of three dimensions without resorting to holograms. All 3D movies work by delivering two pictures, one to each eye. The hard part has always been making sure that only one image reaches each eye. The earliest 3D movies achieved this superimposing the two pictures on top of each other and tinting each one a different color producing what is called an Anaglyph image. But, this method does a rather poor job of perserving colors.

By the 1950s, polarization had become the dominate method of separating images. Theaters would have two projectors running at the same time, with a linear polarizer over each lens. The orientations would be orthogonal to each other, typically at 45 and 135 degrees.^[5] The audience would all have glasses oriented the same way which would only let the correct image through to each eye. The problem with this system is that images will bleed into each other if you tilt your head even slightly, which could cause headaches for people. This method was also popular in the 80's.

For the current generation of 3D movies, the technology has shifted to circular polarization, which takes care of the orientation problem. No matter how you tilt your head, none of either image should bleed into the other.^[6] This technology is currently produced by RealD and accounts for 90% of the 3D market. RealD has produced a circular filter which can switch between clockwise and counter-clockwise polarization very quickly so that only one projector is needed instead of two.^[7]

Pictures

1. "Physics NO. 1 : The momentum of light" Ranza's Place. 29 Jun. 2008. 23 Apr. 2011. http://masteranza.wordpress.com/2008/06/29/the-momentum-of-light/.  ↩

2. "Operation Deep Scope 2005: Mission Plan." Ocean Explorer. NOAA, 26 Aug. 2010. 24 Apr. 2011. http://oceanexplorer.noaa.gov/explorations/05deepscope/background/polarization/media/polarization_img.html.  ↩

3. "Polarizer" Wikipedia. 23 Apr. 2011. http://en.wikipedia.org/wiki/File:Circular.Polarization.Circularly.Polarized.Light_Left.Hand.Animation.305x190.255Colors.gif.  ↩

4. Noritake 23 Apr. 2011. http://www.noritake-elec.com/includes/images/uVersion/how_LCD_Works_450x350.gif.  ↩

5. "Subpixel Rendering" Wikipedia. 21 Jan. 2008. 23 Apr. 2011. http://en.wikipedia.org/wiki/Subpixel_rendering.  ↩

6. "Polarizing_filter_(Photography)" Wikipedia. 29 June 2009. 25 Apr. 2011. http://en.wikipedia.org/wiki/File:Reflection_Polarizer2.jpg.  ↩

7. "What is Stereo Vision?" Optometrists Network. 2010. 22 Apr. 2011. http://www.vision3d.com/stereo.html.  ↩

8. "Forward Motion Theater" New York Stereoscopic Society. March 2, 2008. 22 Apr. 2011. http://www.ny3d.org/2008/03/forward_motion_theater_to_cele_1.html.  ↩