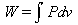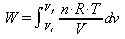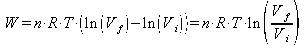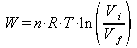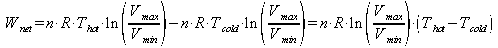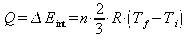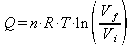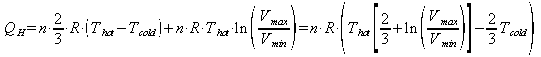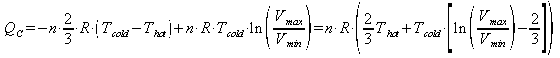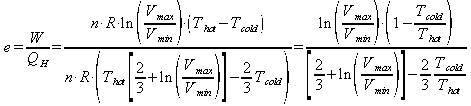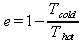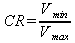Physics Theory
The sterling cycle uses 2 isothermal processes and two isovolumetric processes. Because no work is done during isovolumetric processes the work out is the work done in the isothermal process. The definition of work done by a gas is:
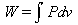
using the ideal gas law to replace P the equation becomes:
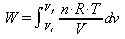
Because n R and T are constants, for an isothermal process, they can be pulled out of the integral and the equation becomes:
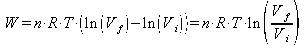
The work done on the gas is simpily the negative of the work done by it. Using properties of logarithms the equation becomes:
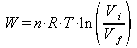
Work is done by the gas when it expands isothermally and work is done by it when it is isothermally compressed, so the total work done is the difference between the work done by the gas when it expands and the work done on it when it contracts:
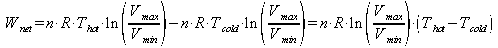
Heat is added by increasing the pressure isovolumetrically and expanding isothermally. For an isovolumetric process:
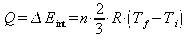
For an isothermal process the heat transfered is equal to the work done by the gas. So the heat added is:
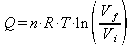
The total heat added in one cycle is:
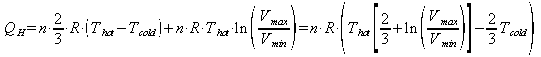
and similarly the heat rejected to the cold reservoir in the rest of the cycle is:
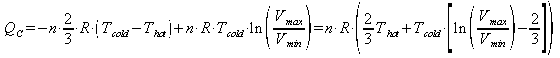
the efficiency of any process is the useful stuff over the energy input. In this case that is the work out over the heat in:
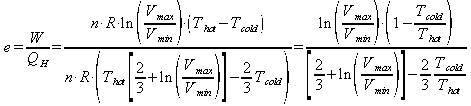
The Carnot engine is a theoretical heat engine that is the most efficent a heat engine that operates on the same temperature difference can be. The Carnot efficiency as given by Serway in chapter 22.4 is:
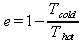
The percentage of the Carnot efficiency that a sterling engine gets is then defined by:

The compression ratio for any engine is simply defined as the minimum volume over the maximum volume. a better discription of compression ratio is provided by Wikipedia
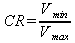
Only the javascript code that runs the PV diagram will be described here. To see the full source right click on a blank part of the P-V page and select view page source. The diagram is drawn in a canvas element. Unfortunately canvas elements can not draw text due to variations in text size so the scale can not be shown.
// get the canvas element using the DOM
var canvas = document.getElementById('diagram');
// Make sure we don't execute when canvas isn't supported
var ctx=null;
if (canvas.getContext){
ctx = canvas.getContext('2d');
ctx.clearRect(0,0,canvas.width,canvas.height);
// use getContext to use the canvas for drawing
}
The canvas element is used to draw the PV diagram. So the first thing that has to be done is to get the element, figure out if the canvas element is supported and clear the canvas. If the canvas element is not supported the only thing that should be skipped is drawing to the canvas.
window.status="";
var outputErr=document.getElementById("error");
outputErr.value="";
var v1=Number(document.getElementById("v1").value);
if(v1<=0){
outputErr.value=window.status="Minimum volume must be greater than zero";
return;
}
var v2=Number(document.getElementById("v2").value);
if(v2<=v1){
outputErr.value=window.status="Maximum volume must be larger then minimum volume";
return;
}
var tc=Number(document.getElementById("tc").value);
if(tc<0){
outputErr.value=window.status="Cold temp must be greater then zero";
return;
}
var th=Number(document.getElementById("th").value);
if(th<=tc){
outputErr.value=window.status="hot temp must be greater then cold temp";
return;
}
var n=Number(document.getElementById("n").value);
if(n<=0){
outputErr.value=window.status="the amount of working fluid must be greater then zero";
return;
}
Next the error outputs (a text output and the status line) are cleared and values are parsed from the input text boxes if an illegal value is found then an error is shown and the function returns
document.getElementById("w-out").value=""+(n*R*Math.log(v2/v1)*(th-tc)).toPrecision(3)+" J";
document.getElementById("q-hot").value=""+(n*R*(th*(2/3+Math.log(v2/v1))-2/3*tc)).toPrecision(3)+" J";
document.getElementById("q-cold").value=""+(n*R*(2/3*th+tc*(Math.log(v2/v1)-2/3))).toPrecision(3)+" J";
document.getElementById("eff").value=""+(100*Math.log(v2/v1)*(1-tc/th)/((2/3+Math.log(v2/v1))-2*tc/(3*th))).toPrecision(3)+"%";
document.getElementById("c-eff").value=""+(100*(1-tc/th)).toPrecision(3)+"%";
document.getElementById("pc-eff").value=""+(100*Math.log(v2/v1)/((2/3+Math.log(v2/v1))-2*tc/(3*th))).toPrecision(3)+"%";
document.getElementById("cr").value=""+(v2/v1);
next the output text boxes are set according to the equations developed in the physics theory above. toPrecision is a function that forces the number to have the specified number of significant figures.
if(ctx!=null){
var vScale=(canvas.width-10)/v2,pScale=(canvas.height-10)/((n*this.R*th)/v1);
ctx.clearRect(0,0,canvas.width,canvas.height);
//draw the center
ctx.beginPath();
ctx.moveTo(v1*vScale,canvas.height-pScale*(n*this.R*tc)/v1);
ctx.lineTo(v1*vScale,10);
this.isotherm(th,v1,v2,n,pScale,vScale,ctx,canvas.height);
ctx.lineTo(canvas.width-10,canvas.height-pScale*(n*this.R*tc)/v2);
this.isotherm(tc,v2,v1,n,pScale,vScale,ctx,canvas.height);
ctx.fillStyle = "orange";
ctx.fill();
//now draw the lines
ctx.lineWidth = 4;
ctx.lineCap = "round";
ctx.lineJoin = "round";
ctx.beginPath();
ctx.moveTo(v1*vScale,canvas.height-pScale*(n*this.R*tc)/v1);
ctx.lineTo(v1*vScale,10);
this.isotherm(th,v1,v2,n,pScale,vScale,ctx,canvas.height);
ctx.strokeStyle = "red";
ctx.stroke();
ctx.beginPath();
ctx.strokeStyle = "blue";
ctx.moveTo(canvas.width-10,canvas.height-pScale*(n*this.R*th)/v2);
ctx.lineTo(canvas.width-10,canvas.height-pScale*(n*this.R*tc)/v2);
this.isotherm(tc,v2,v1,n,pScale,vScale,ctx,canvas.height);
ctx.stroke();
}else if(!this.errorShown){
alert('Your browser does not seem to support the canvas element. Try using Firefox 1.5 or greater or Safari\n'+
'The Text part of the demo will work fine though.');
this.errorShown=true;
}
finally the PV diagram is drawn to the canvas. The diagram is auto scaled so that maximum pressure point is 10 pixel's from the top and the maximum volume point is 10 pixel's from the right. If the canvas element is not supported then an error is shown when the page is first loaded and not shown again so that the text outputs can still be used. In order to color the enclosed area orange and have the processes that add heat be shown in red and processes that reject heat be shown in blue, the path must be drawn twice. once to draw the orange area and a second time to draw the two pairs of red and blue lines which are drawn as two separate paths.
isotherm : function(t,vi,vf,n,pScale,vScale,ctx,h){
var num=1000;
for(var i=0,v=vi;i<=num;i++,v+=(vf-vi)/num){
ctx.lineTo(v*vScale,h-pScale*(n*this.R*t)/v);
}
}
This function is used to draw isotherms on the P-V diagram. Originally an attempt was made to use Bézier curves but that failed so this function was created which uses lots of little lines to approximate a curve. num is the number of lines to break the process into. The function takes 8 parameters : the temperature of the isotherm, the initial and final volumes, the number of mols of gas in the engine, the scales for the pressure and volume axises, the drawing context for the canvas and the height of the canvas in pixels.
init : function(){
var canvas = document.getElementById('diagram');
if(canvas.getContext){
canvas.width=document.width-4;
canvas.height=(0.7*document.getElementById('page').clientHeight);
}
this.drawPV();
}
This function is used to set the size of the canvas element. The canvas element can be resized using CSS but when this is done the image is simply scaled and the result can look quite poor if the computed area is larger then the original area. The result is that the P-V diagram fills the width of the page (the -4 is to account for the 2 pixel border) and takes up about 70% of the height.