The eccentricity is simply how elliptical the Earth’s orbit around the sun is. Based on Kepler's first law of planetary motion, it can be mathematically described as: e2 = 1 - y2/ x2 |
 |
modified
from http://www.doc.mmu.ac.uk/aric/gccsg/figures/2_1.html |
|
Perihelion is the moment when the Earth is the closest to the sun in its orbit. Aphelion is the moment when the Earth is the farthest away from the sun. |
|
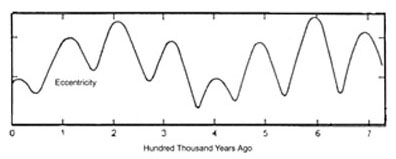 |
The gravitational force exerted by Jupiter causes the Earth’s orbit to vary from nearly circular with an eccentricity of 0.005 to quite elliptical with an eccentricity of 0.06. Currently, we enjoy an eccentricity of 0.0174, nearly its minimum. There is only a 3% difference in the distance to the sun at perihelion and aphelion. |
graph from GEOS 416 class notes |
|
When eccentricity is maximized, there is almost a 12% difference. Eccentricity has two periods, one of 100,000 years that corresponds with the twenty glacial-interglacial cycles seen in Pleistocene sediments, and one of 400,000 years. When the Earth’s orbit is highly elliptical, either the northern or southern hemisphere basks in very hot summers and freezes in very cold winters while the opposite hemisphere experiences cool summers and warm winters. Since the sun emits radiation in all directions, Lowrie (1997) explains that “At a distance r [the sun] floods a sphere with surface area of 4(pi)r2. Thus, solar insolation decreases as the inverse square of the distance.” Because of this, there can be up to a 30% difference in the amount of solar radiation the Earth receives between perihelion and aphelion. |
|
 |
 |
 |
 |
 |
 |