Basic Conditions of a
Superconductor
Superconductivity can be destroyed if a sufficiently
strong magnetic field is applied. A metal in this state has very unique
magnetic properties that are unlike those at normal temperatures. A superconductor
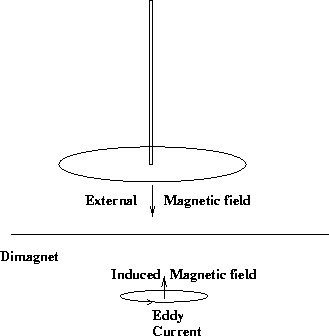
is often referred to as the perfect diamagnetic. Diamagnetic, ideally,
are a class of materials that do not conserve magnetic flux, but expel it.
A superconductor is classified as a perfect diamagnetic because by all measurable
standards the magnetic flux within the material is zero.
Electrons have a wave-like nature so
an electron moving through a metal can be represented by a plane wave progressing
in the same direction. A metal has a crystalline structure with the atoms
lying on a repetitive lattice; a plane wave can pass through a perfectly periodic
structure without being scattered into other directions. An electron is able
to pass through a perfect crystal without any loss of momentum of its original
direction. That is why it is important for superconductors to have very
low impurities; any fault in the periodicity of the crystal will scatter
the electron wave and introduce some resistance. This is called the residual
resistance and it is independent of the temperature.
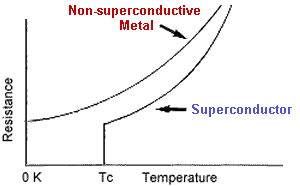
Thermal vibrations also increase the
resistance so when the temperature is lowered, the thermal vibrations of
the atoms decrease and so the electrons are less frequently scattered. In
short, the resistance of a metal is dependent on the purity of a metal and
its temperature: metals with few impurities reach a superconducting state
at low temperatures.
The superconductivity state of a metal exists only
in a certain range of temperature and field strength. As stated earlier,
a large magnetic field can destroy a superconductor. The condition for the
superconducting state to exist in the metal is that of some combination for
the superconducting state to exist in the metal is that of some combination
of the temperature and the magnetic field strength. The critical values of
the magnetic field strength and temperature are related by the following
equation:
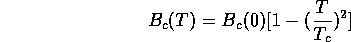
where H(c) is the critical field strength at the temperature T, H (0)
is the maximum critical field strength occurring at absolute zero, T(c)
is the critical temperature – the highest temperature for superconductivity.
There are also other basic conditions for superconductors and they can
be explained by BCS Theory.
BCS Theory
John Bardeen, Leon Cooper, and Robert Schreiffer proposed
the first major microscopic theory in 1957, now known as the BCS theory .
Using this theory, one starts with the concept that superconductors, in
a non-superconducting state, possess electrons that even under normal conditions
are not susceptible to resistivity. Under the condition of low temperature
and sometimes high pressure, these electrons tend to pair together to form
Cooper pairs, often referred to as superelectrons. These superelectrons,
therefore have a both a charge and mass that is twice that of a normal electron.
It is these superelectrons that possess the perfect conduction observed
in superconductivity. According to the BCS theory, as the temperature
of certain materials decreases, the density of these pairs increases.
This in turn, will increase the amount of superelectrons ready to conduct
a perfect current.


