Magnetic fields surround any magnetic substance. They are "produced by electric currents"(http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magfie.html#c1). They are usually represented as lines as in the pictures below. (Courtesy of http://www.sciencetech.technomuses.ca/english/schoolzone/Info_Magnets.cfm#whatare).

<--Attract || Repel-->

As you can see the dotted lines are representing the force fields. These are 3 dimensional and travel all around an object like so (courtesy of http://www.sciencetech.technomuses.ca/english/schoolzone/Info_Magnets.cfm#whatare)

It is also important to note that these magnetic fields always travel from the north pole to the south pole. Magnetic fields always radiate out of the north pole and magnetic fields always go in to the south pole. We define a magnetic field with the symbol B. "The direction of the magnetic field B at any location is the direction in which the compass needle points at that location" (Serway). We know the magnetic force by the equation and picture below provide by (http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magfor.html)

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magfor.html also gives the implications of the expression.

"1. The force is perpendicular to both the velocity v of the charge q and the magnetic field B.

2. The magnitude of the force is F = qvB sin where is the angle < 180 degrees between the velocity and the magnetic field. This implies that the magnetic force on a stationary charge or a charge moving parallel to the magnetic field is zero.

3. The direction of the force is given by the right hand rule. The force relationship above is in the form of a vector product.

From the force relationship above it can be deduced that the units of magnetic field are Newton seconds /(Coulomb meter) or Newton's per Ampere meter. This unit is named the Tesla. It is a large unit, and the smaller unit Gauss is used for small fields like the Earth's magnetic field. A Tesla is 10,000 Gauss. The Earth's magnetic field is on the order of half a Gauss. "

Although the right hand rule is linked above I felt it important to put the picture below just because it is a concept often used when calculating magnetic field problems. (Image provide by: http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magfor.html)

This picture demonstrates two methods of the right hand rule, the one I've seen used most often is the one on the left.

With regard to the velocity of a particle moving through a magnetic field, its direction can be changed by the field but speed and kinetic energy of the particle cannot be altered by the magnetic field. It is also important to note that "when a charged particle moves in a magnetic field, the work done by the magnetic force on the particle is zero." We know this" because the displacement is always perpendicular to the direction of the force"(Serway). Think of it as if you were walking. The work done while walking is zero because you are displacing forward and the direction of the force is down (your feet striking down on the ground pushing you up).

If we are dealing with a charged particle in a magnetic field, the particle moves in a circle perpendicular to the magnetic field. It moves in this way because "the magnetic force F sub b is at right angles to v and B and has a constant magnitude qvB" (Serway). The force is deflecting v and F sub b continuously. However, note that again although the direction of the velocity changes, it does not change its magnitude. A really cool webpage related to magnetic forces on moving charges can be found here. Depending on weather the magnetic field goes into or out of the "circle" determines which direction the particle moves. If the field is coming out of the page the particle moves in a clockwise fashion. If the field is going into the page the particle travels counterclockwise. This page provides a real time demonstration of this. Same is true depending on the charge. If the charge is positive(and the force is pointing inward) it would move counterclockwise, and if the the charge is negative (and the force is pointing inward) it would move clockwise. Below is a visual and the equations for determining radius and velocity.

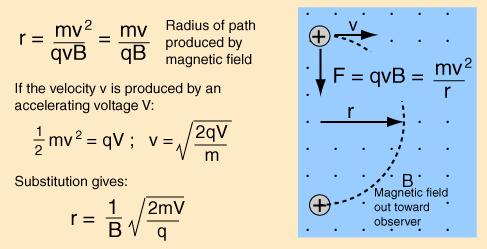
(Image Courtesy of http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/maspec.html#c2)

Please continue the discussion of magnetic fields here.