Navigation Hub

Harmonics and cool math

Harmonics

In other sections, we gave an overview of the natural frequencies of an object. Someone who plays a stringed instrument would be able to change the natural frequency of their instrument by changing the length of one or more of their strings. There is a particular relationship between the length of an instrument's string and the frequency of sound it produces. That is... fn = v/λn = nv/2L When n=01 this is the fundamental frequency and the lowest note that could be produced by an object. When n=2, we have the second harmonic frequency. When n=3, we have the third harmonic frequency, and so on. 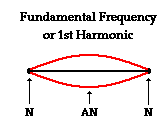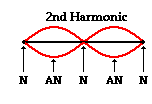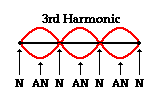From the pictures, we see that each harmonic adds one node and one antinode to the standing wave pattern.

Ratios between Harmonics

Knowing some of the basic physics behind sound frequencies, we can put a lot of physical meaning behind terms that are thrown around in music theory. The following is a table relating whole number ratios of frequencies to terms used in music. "3:2, perfect fifth 4:3, fourth 5:3, major sixth 5:4, major third 6:5, minor third 8:5, minor sixth" These are only a very select few terms taken from all of music theory. Entire textbooks could be written on that subject, and if it interests you I'd highly encourage further reading on the subject.