Paintball guns shoot at relitively slow speed, unlike a bullet that will drop several inches over a shot, a paintball will drop several feet
        depending on the distance.
        Think of it like somewhere inbetween throwning a ball and shooting a rifle. Some angle of launch must be calculated to adjust for the
        the pull of gravitiy.

        First we can look at the ideal conditions for a shot. ie no air resistance, level ground.

        We know initial velocity is 300 fps, gravitiy is 32 ft/s^2, and we also know that 45 degree angle will produce max distance.
        Take upward to be positive Y axis and right to be Positive X axis

        To find the Maximum Ideal Range of the Weapon we solve

        Y=Yo+VoSin(45)(t)-(1/2)(32)(t)^2
        t=time    Y=height    Yo=initial height    Vo=initial velocity

        Lets Assume that the person shooting and the target are both the same height
        Meaning the contact point and launch point are equal height to the ground

        0=0+300sin(45)t-(16)(t^2)
        t=13.26 seconds of flight
       
        Now to find the distance covered in 13.26 seconds

        X=Xo+VoCos(45)(t)
        t=time    Vo=inital velocity    Xo=Starting position

        X=0+300Cos(45)(13.26)
        X=2812.5ft

        Now remember this problem did not take air resistance into account.
        Since there is no need for shooting 2500 ft in paintball ball lets take a realisitic problem.

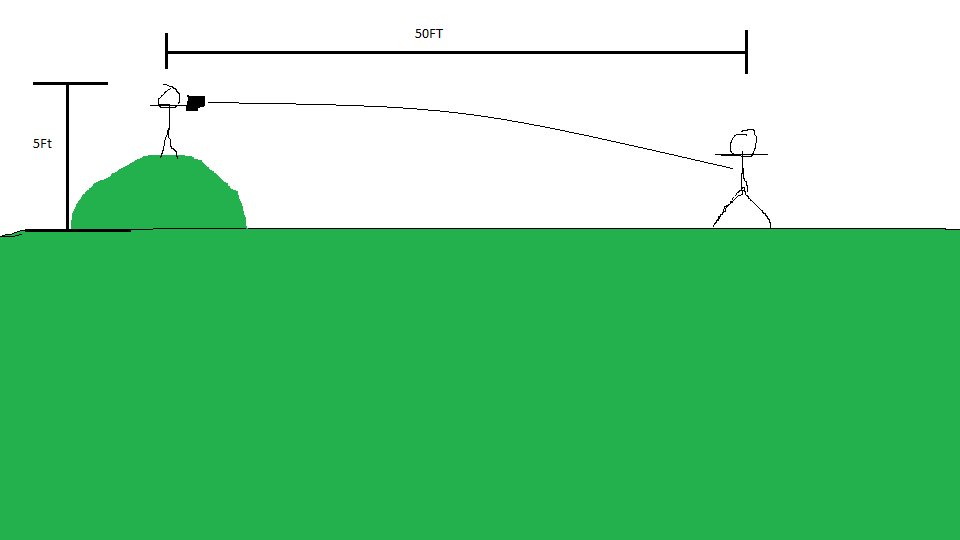
        You are shooting at a person 50 ft away while standing on a hill of 5 ft tall what angle do you need to aim to hit him?

        For this question we solve a system of two equations

        50=300Cos(angle)t
        0=5+300Sin(angle)t-16(t)^2

        Solving these two equations give you an the answer angle = -5.21 degrees