What
is
the
Magnus
effect
and
how to calculate it:
The Magnus effect uses principals from Bernoulli's equation.
Bernoulli's equation states that if the velocity of a moving fluid
increased,
the pressure must decrease. (at ideal conditions, constant elevation)
Bernoulli's equation with constant
elevation:
P+(1/2)dv^2=
C ......(eq.1)
In
solving for P we get:
P=C-(1/2)dv^2
......(eq.2)
Where
P =Pressure
d=The
flowing
fluid
of
constant
density
v= Velocity of the
fluid
C=
constant
From Equation 2 we can see that
pressure on the system is reduced when
velocity is increased.
This is how an airplane wing creates
lift. Air is forced to
travel a longer distance over the top of the wing than the air
underneath. The air above the wing is being forced to cover a
greater distance in the same amount of time as the air passing under
the wing. This in turn means that the velocity of the air above
the wing is greater than that passing under. This velocity difference
leads to a pressure difference, high pressure under the wing, low
pressure above the wing. This difference in pressures causes
lift.
The Magnus Effect
Spinning
objects
traveling
through
a
viscus fluid act much like an
airfoil (airplane wing)
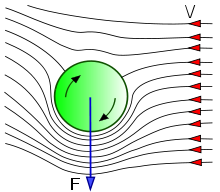http://schema-root.org/science/physics/effects/magnus/magnus_effect.png
First described in 1852 by Heinrich
Magnus, the Magnus effect is a
force generated by a spinning object traveling through a viscus
fluid. The force is perpindicular to the velocity vector of the
object. The direction of spin dictates the orientation of the
Magnus force on the objecc. The orientation of the force can
change but it is important to remmeber that it is always perpindicualr
to the direction of fluid.
Like an areofoil the rotation of the
object forces some air to take a
longer path around the spinning object. This air moves faster to
cover the greater distance around the object in the same amount of
time. The image above shows a ball rotating clockwise, we can see
that the airstreams are pulled under the ball by its rotation.
The resulting Magnus force is in the downward direction perpindicular
to the direction of the air.
The force of the Magnus effect can be
calculated with the following
equation:
Fm = S (w × v)
Where:
Fm =the Magnus force vector
w=
angular
velocity
vector
of
the
object
v=Velocity of
the fluid (or velocity of
object, depends on perspective)
S= air resistance coefficient
across the surface of the object
Once Fm
is found we can use the basic kinematic equations to predict the
characteristics of spinning objects in flight.
Utilizing the Magnus Effect
in Sports Home
Bibliography
Modern
Technologies Using The Magnus Effect
