
Spins, Flips
and the Laws of Inertia
When
it
comes to riding, there’s nothing like mastering that new trick. A
common area
of
interest between professional and novice
riders alike is new arial flips and spins. Well
my
friends, let the laws of physics ease your mind as you
conquer new
spins and flips. The topic of this page is revolved around the physics
of rotational
motion, more specifically, a little
something called the moment of inertia.
Moment of inertia is defined as the characteristic
dispersion of mass
troughout a spinning object. As it turns out, controlling ones’ moment
of Inertia is
a great
way to control motion during rotational motion similar to the kind
experienced during a spin or flip, let's explore... All objects that
are moving and possess mass also possess momentum this fact is modeled
in the equation p=mv for linear motion, but it also applies to objects
in rotational motion. Just like linear motion, a spinning objects'
momentum is conserved and is modeled by the equation L=Iw
.
The
law
of angular momentum conservation states that the angular velocity of an
object is
dependent
on the moment of inertia (granted constant mass). As a rule of thumb,
the
farther from
the center of mass an objects’ weight lies, the larger its’ moment of
inertia.
The Law of conservation of momentum is portrayed
by the equation Iw(intial)=Iw(final),
where Iw=L (angular
momentum).
This law of motion has valuable implications to
the world of a snowboarder. The consequence is that for angular
momentum to
be conserved, the variables on either side must even out to give a
steady
number. This means that as the moment of inertia changes, angular
velocity must also fluxuate to
maintain
constant momentum. So in effect, as a moment of inertia decreases,
an object gains angular velocity to compensate likewise, when
inertia increase angular velocity must decrease accordingly. Knowing
this law, we are able to form a few well founded guidelines for
approaching and excecuting high caliber spins.
· Steps to pulling off a high grade spin
1.) At the last moments prior to leaving the end of the ramp, dig your edge in to direct your board parallel to the jump in a curved motion, the direction of your spin. Simultaneously pre-winding your torso and arms in the opposite direction of spin to supply the torque in the following step.
2.) The instant your board leaves the end of the ramp, release your pre-wound torso like a spring, supplying as much force from this motion as possible. Your body should be at about 2/3 height at this position. At this instant your body has a relatively large moment of inertia, so the angular velocity is not optimized at this point in flight.
3.) Tuck up your legs and suck in your arms, this motion will lower your moment of inertia and cause an increase in rotational velocity.
4.)
Drop
the landing gear. With only a second or two to spare, let
your
arms come out and legs drop down while keeping an eye out for your
landing.
This will slow your rotational motion and have a stabilizing effect on
your
course of flight. Remember that a second or so is all you need to
drastically
reduce rotational motion. Be sure not to unwind too early, as it is
difficult
to maneuver in the air once you have. Slightly tucked legs at the end
of a
landing can also act as a cushioning spring, a nice thing to have at
the end of
a long fall. The low friction forces allow riders to quickly transfer
the
energy towards motion instead of say, the riders’ bone structure.

Where's the prove you ask, let's see an example...

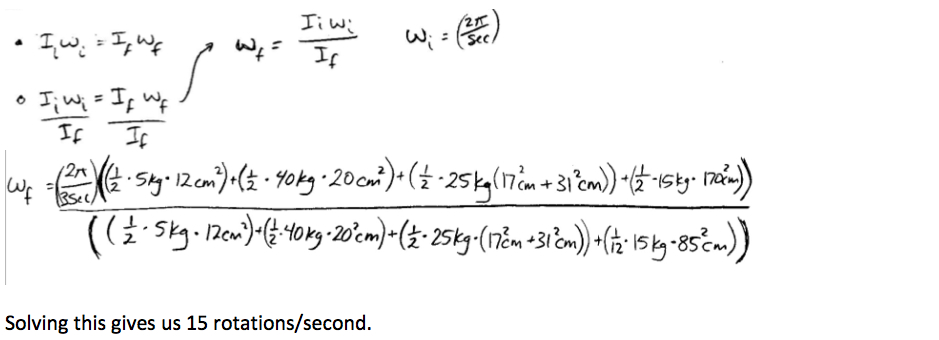
This example
reveals a remarkable increase in rotation. Indeed it may even seem
excessive, remember however that the equation does not account for air
drag and mass dispersion may not be true to life (i.e. 15 kg arms are
too heavy). We must also keep in mind that rotational motion requires
energy. His kinetic rotational energy will thus diminish over time,
since there is no permanant acceleration supplying determining
rotational velocity. The principle however, remains true to life and
accounting
for this law can dramatically improve your spin game, keep it in
mind.