
When a rider stops on a slope, he/she possesses potential energy but
his/her
kinetic energy is at a standstill. The rider possesses a potential
energy at any point is equal to; (the
height of the mountain) x (mass of the rider) x (acceleration of
gravity)
(g=9.81 m/s²). This is denoted in the equation U=mgh. When the rider points his/her
forward edge
down the
slope again, potential energy is rapidly converted into kinetic
energy once again. Kinetic energy is defined by the equation K=(1/2)mv². Together potential
and kinetic energy are used to explain a physical concept called work
(work equals force over distance), and the subsequent energy equations
have tremendous relevance to the sport of snowboarding.
Suppose we wish to find the velocity that must be reached to achieve a
certain height in a halfpipe competition. We can use the laws of
conservation of energy to solve this problem through simple
manipulation of the statement mgh=(1/2)mv²
(Ui=Kf).
This equation is restricted to circumstances where the rider starts
from stand still and does not slow movement during descent, i.e. 100%
of potential energy is transfered into kinetic.
When we solve this equation with a little algebra we find that v=squareroot[2gh], which means
simply plugging in the desired height and acceleration of gravity we
can give a good approximation of the speed necessary to achieve this
height. This works because we know that any potential energy stored by
the rider at peak height must come from the kinetic energy of his
movement in the pipe. Since we know the height we want to achieve and
the acceleration of gravity we can easily find the velocityhe/she needs
reach. This is an approximation however, so it is important to realize
that this equation neglects the effects of friction and wind
resistance.
On a slope of negligable friction and wind resistance however, (nice
day and board waxed) the
rate of conversion of potential to kinetic energy (A.K.A. acceleration)
depends primarily on slope. Motion of any object from rest requires
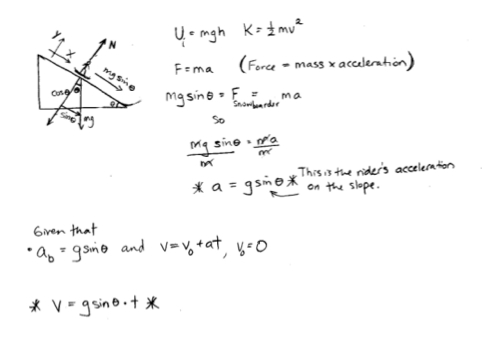
force, refered to as the force of movement, it is a consequence of
Newton's second law of motion F=ma,
one
of
the most respected principles in all of physics.
When
decending a slope it is important to know that the acceleration of
gravity has not changed, it is however taking a different path which
results in slower acceleration compared to freefall, in this case given
by the representation
a=gsin(theta). Given this newly aquired acceleration, we can
estimate the riders' expected velocity. This is an important thing to
know and we can use it to find a variety of physical qualities the
rider may possess at a given moment. And when you know your cards, it
is easier to play them. These energy and work equations are
tremendously useful in situations that even the average rider faces on
a regular basis.

