Calculations of Ideal Projectile Motion
Surprisingly enough, physics actually allows us to calculate how a ball projected into the air, assuming no air resistance, will behave. According to the kinematic equations, calculating the distance traveled, maximum height, and even the total time that the ball is air borne is quite simple. However, we will not need to calculate all of those variable. The distance traveled is the true component of interest here.
A few important kinematic equations in this situation are: Xf = Xi + Vt, and Yf = Yi + Vt + .5gt^2. In the first equation listed, "Xf" is the final position, "Xi" is the initial position, "V" is the velocity, and "t" is the time it takes to travel from "Xi" to "Xf". In the second equation, "Yf" is the final height, "Yi" is the initial height, "V" is the velocity, "t" is the time from "Yi" to "Xf", and "g" is the acceleration constant. As we see in the picture below, which symbolizes a baseball hit in an ideal case, the initial and final height of the ball are equal. The difference between the final position and the initial position, Xf - Xi, is the range or distance the ball traveled. The range, "R", can be derived from these two kinematic equations, and is as follows: R = (Vi^2sin2&)/g. As we see, "Vi" is the initial velocity, "&" is the angle between the ground and the ball's projection, and "g" is the downward acceleration. If you notice, the maximum range can be accomplished if the angle is 45 degrees. This is because 45 times 2 is 90, and sin90 is 1 (Lowry 91-95).
http://www.geneseo.edu/~pogo/Analyt1Labs/Labphotos/Projectile.htm
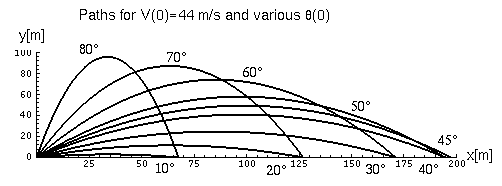
http://carini.physics.indiana.edu/E105/projectile-range.html
By analyzing the graph above, we can better imagine the differences in the range by simply changing the angle from where the ball was launched. Also note that the same distance can be achieved at different angles, for example, a ball hit at an angle of 70 degrees travels the same distance as if it were hit at 20 degrees from the horizontal. However, a ball projected at 45 degrees travels the furthest distance. Remember, that these graphs are examples of objects traveling through airless mediums.
Calculation
Lets do a simple calculation! Using the formula, R = (Vi^2 sin2&)/g we can calculate what velocity we would need to launch a baseball a distance of 500 feet. We will assume that the ball is hit at an optimum angle of 45 degrees and obviously the constant "g" will remain at 32ft/s^2. Substituting these values into the formula we get, 500ft = (Vi^2 sin90)/(32ft/s^2). Solving for "Vi", we find the initial velocity of the ball rebounding off the bat must be 126 feet per second. This velocity converts to 86 mph. As we see, it is not necessary for the velocity to be very large to travel 500 feet. However, all these calculations were done neglecting air resistance.
![]()
![]()