Projectile Motion with Air Resistance
Unfortunately, the real world is more complex than what we desire sometimes. In a real situation, unless you are playing on the moon, a baseball flying through space encounters resistive forces from the air. These resistive forces greatly complicate matters, and that is why most beginning physicists, such as myself, neglect them. Instead of discarding the issue, however, we will examine and explore deeper into this problem.
http://www.geneseo.edu/~freeman/animations/realistic_baseball_trajectory.htm
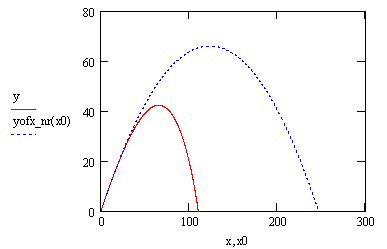
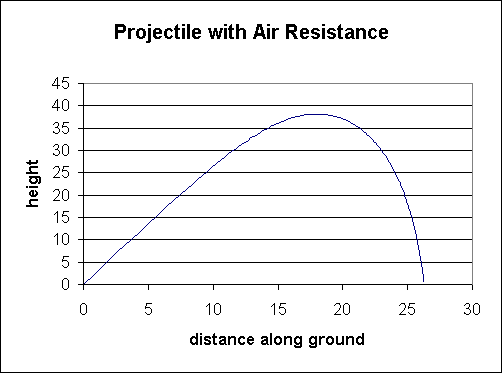
From studying the above graph, we can obviously conclude that air resistance causes a profound difference in the path of a ball. According to this particular graph, the distance that the ball traveled with a resistive force at some initial velocity, V, traveled about half the distance of the ball without air resistance. The main cause of this resistance is the surface area of the baseball against the air, which is 6.61 square inches. Another factor is actually the density of the air which varies throughout the atmosphere, but such a change in density would be ignored (Carmichael 2003).
http://galileo.phys.virginia.edu/classes/581/ProjectilesExcel.html
Calculation
The only possible technique to create a position function of the ball with respect to time with the complication of air resistance is by solving a differential equation. Using physics concepts that explains the diagram below, we are able to create a simple equation: mg - kv = ma (Mathews 1998). The variable "m" is the mass, "g" is the acceleration due to gravity, "k" is the constant of proportionality due to the velocity, "v" is the velocity of the ball, and "a" is the acceleration of the mass after the effects of the air resistance. Rearranging the variables and differentiating the acceleration and velocity , we find that the equation is: d^2x/dt^2 + (k/m)dx/dt - g = 0. To determine the position of the ball in terms of "t", it is necessary to solve this differential equation. With air resistance the initial velocity of the baseball would need to be 152 mph or 223 feet per second at an angle of 45 degrees in order to carry a distance of 500 feet, much greater than 86 mph calculated earlier (Giordano 28-30).
To view the calculation process and the equation itself, click here.
velocity

drag
gravity
http://library.thinkquest.org/11902/physics/range.html