Phys 211
Physics Behind Electric Guitars:
The Wave Equation:
Certain laws in physics can be described by using partial differential equations. One such equation, the wave equation, is especially useful for quantifying the movement of a wavelength. This could be a wave in the water, a sound wave, an electromagnetic wave, or a wave along a vibrating string. In particular, we want to study the latter case. (Stewart, p. 953)
The wave equation can be expressed by any equation having the form:
Read as, "The second partial of 'u' with respect to 't' is equal to some constant 'a' squared times the second partial of 'u' with respect to 'x'
Physics Behind Electric Guitars:
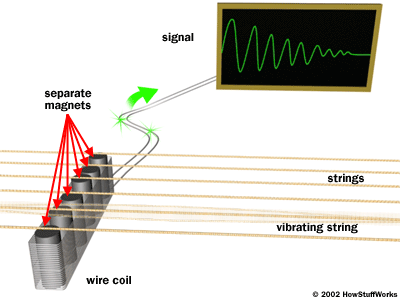Image:
Image taken from howstuffworks.com
Physics Behind Electric Guitars:
Introductory Ideas:
Before delving into the core physics of electric guitars, some basic information must be understood. These ideas will be discussed more thoroughly later on in this section.
- Sound from an electric guitar is produced by electromagnetic pick-ups that sense vibrations in the strings electronically and route the electronic signal to an amp and speaker.
- The vibrations of the strings can be quantified and calculated according to basic laws in physics. These include certain relationships between velocity, wavelength, and frequency and equations that describe the motion of a string fixed at both ends.
Physics Behind Electric Guitars:
Waves on a String:
Sam Hokin, the author of "The Physics of Everyday Stuff", explained how guitars employ these two relationships this way:
"Since the fundamental wavelength of a standing wave on a guitar string is twice the distance between the bridge and the fret, all six strings use the same range of wavelengths. To have different pitches (frequencies) of the strings, then, one must have different wave speeds. There are two ways to do this: by having different tension T or by having different mass density u (or a combination of the two). If one varied pitch only by varying tension, the high strings would be very tight and the low strings would be very loose and it would be very difficult to play. It is much easier to play a guitar if the strings all have roughly the same tension; for this reason, the lower strings have higher mass density, by making them thicker and, for the 3 low strings, wrapping them with wire." (Hokin, n. p.)
Physics Behind Electric Guitars:
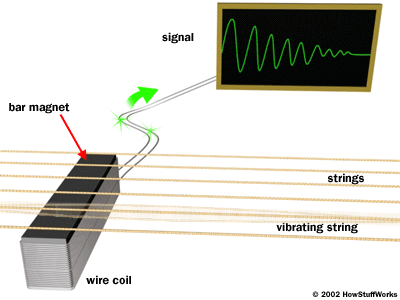Image:Electromagnets can turn electrical energy into motion. Likewise the converse is true: they can turn motion into electrical energy.
Such is the case with electric guitar pick-ups.Image taken from howstuffworks.com
Physics Behind Electric Guitars:
How Pick-Ups Work:
Electric guitar pick-ups work by employing "principles of magnetic induction." The pick-ups are composed of small electromagnets (magnets that are wrapped with a coil of wire, thus allowing an electric current to flow through them). Because of their close proximity to the strings, these magnets induce a north and south pole on the strings. When the string is played, it begins to oscillate, or move in a wave-like fashion. This affects the field surrounding the pick-up and causes a change in the magnetic field. These changes, or fluctuations in the magnetic field are transmitted through the wires connecting the pick-up(s) to the output jack and are thus relayed to the amplifier where they are sent to the speaker and converted from electrical energy once again into motion energy (sound). (Brain, n.p.)
Physics Behind Electric Guitars:
Waves on a String:
A guitar string is an example of "a string fixed at both ends which is elastic and can vibrate." Such vibrations are called standing waves, and all of them satisfy "the relationship between wavelength and frequency that comes from the definition of waves." (Hokin, n.p.)
Where 'v' is the velocity of the wave, 'f' is the frequency, and 'lambda' is wavelength.
The speed of the wave depends on two factors: the tension 't' and the mass density of the string (mass/length) 'u'. This gives us another relationship:
Physics Behind Electric Guitars:
Waves on a String:
2nd Overtone (l = 3/2)
3rd Overtone (l = 4
4th Overtone (l = 5
Physics Behind Electric Guitars:
Waves on a String:
Any wave that has its nodes (points at which it intersects the axis of oscillation) at the ends of the string can exist on a guitar. To illustrate this fact, refer to the following illustrations taken from Hokin's web site.
Fundamental (l ="The fundamental satisfies the condition l =
1st Overtone (l =2"The 1st overtone satisfies the condition l =
Physics Behind Electric Guitars:
The Wave Equation:
"If u(x,t) represents the displacement of a vibrating violin string at time t and at a distance x from one end of the string, then u(x,t) satisfies the wave equation." (Stewart, p. 953)
Physics Behind Electric Guitars:
Fret Spacing:
It is commonly known that frets (bars that "divide" the string into sections of certain lengths) get closer together towards the bridge of the guitar. This is due to the fact that "each successive note is r = 1.0595 higher in pitch" and the fact that the velocity of the waves is held constant on a given string. So given an open string of length 'l' we can determine the fret spacing from this. (Hokin, n. pag.)
"The first fret must be placed l/1.0595 from the neck, the second fret a distance of l/1.0595^2, and so on." (Hokin, n. pag.) Thus this gives us the relationship:
Where D is the distance from the neck, l is the length of the string, and n is the number of the fret starting with 1 (the fret closest to the neck).
Physics Behind Electric Guitars:
Synopsis:
- Frets are spaced out according to this relationship:
Where D is the distance from the neck, l is the length of the string, and n is the number of the fret starting with 1 (the fret closest to the neck).
Physics Behind Electric Guitars:
Synopsis:
While there are many other aspects of electric guitars (i.e. methods of amplification, effects, etc.), a good grasp of the physics involved in electric guitars can be obtained by bearing in mind the following:
- Electric guitars use pickups to convert motion energy into electrical energy. This electrical energy is processed and amplified by an amp and outputted to a speaker where it is converted back into motion energy (i.e. sound).
- Velocity of a wave is equal to frequency x wavelength. Since all the strings use the same range of wavelengths, in order to produce different frequencies (pitches), velocity must be varied.
- Velocity is varied by changing either linear mass density and/or tension in the string. It is desirable to play a guitar with nearly uniform tension from string to string, thus strings are of varying masses.
