Calculus
Newton took his first step beyond his mentors during the winter of 1664-5. During this time, Newton extended the use of Willis's infinite series to evaluate areas and developed what we now know as the binomial theorem. In Newton's studies he generalized Pascal's Binomial Theorem to fractional and negative powers (Westfall 42).
The Binomial Theorem
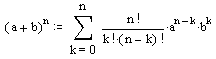 |
Newton also discovered the concept of decimal
fractions, which could be used to evaluate Pi out to any given number of decimal
places. Newton believed that quantities calculated by binomial expansion should
be considered an infinite series. Adding the binomial theorem to this concept
of infinite series, Newton found that a difficult quantity that he wanted
to square could be expressed by an infinite series that was squared term by
term. This discovery enabled him to find the area under almost any algebraic
curve in mathematics and became known as the fundamental theorem of calculus
(Westfall 42).
Fundamental Theorem of Calculus