Lift
One of the most important concepts to understanding
how a hang glider works is to understand the concept of lift force. This
lift force is best explained through use of Bernoulli's equation. This
equation looks like this: P + 1/2þv2 = constant, where
þ is the greek letter rho, meaning the density of the fluid (air in
this case), v is the velocity, g is the gravitational force, and P is the
air pressure. This equation relates pressure and velocity and in simple
terms means that if that velocity increases, the pressure must decrease,
and vice versa so that the equation remains constant.
To understand the lift force on a hang glider, this equation must be applied to a wing. Wings are shaped so that as air flows over the top of them, its velocity must increase and results in a greater air speed on top of the wing than on the bottom. And from Bernoulli's equation, we can see that if velocity increases, pressure must decrease. This means that air pressure is higher on the bottom of the wing than on the top, and an upward force known as lift results. Maybe this illustration will help you to visualize this effect:

To understand the lift force on a hang glider, this equation must be applied to a wing. Wings are shaped so that as air flows over the top of them, its velocity must increase and results in a greater air speed on top of the wing than on the bottom. And from Bernoulli's equation, we can see that if velocity increases, pressure must decrease. This means that air pressure is higher on the bottom of the wing than on the top, and an upward force known as lift results. Maybe this illustration will help you to visualize this effect:
Image produced by Nathan Earls
Another factor influencing lift is commonly known
as the angle of attack. This is simply the upward tilt of
the wing. In general a greater angle of attack means that more lift
is generated because the air must flow faster to get over the top of the
wing. A greater angle of attack also helps to increase lift because
air is deflected off of the bottom of the wing, and the air exerts an upward
force on the wing. This applies when the angle of attack is increased
up to about 16 to 20 degrees above horizontal depending on the application.
When the angle of attack is too great, the air flow over the top is
no longer smooth and becomes turbulent. This causes the pressure difference
across the wing as described by Bernoulli's equation to drop and lift decreases
dramatically. This effect is called stall.
The lift force can be calculated by this equation: L = 1/2CLþAv2, where L is the lift force, CL is the coefficient of lift (which varies according to the shape of the wing), þ is the greek letter rho meaning air density, A is the cross-sectional area of the glider, and v is the velocity of the glider. This is very similar to the equation for drag, which is discussed in the next page. You can that the lift force is proportional to the square of the velocity. Now this is important because sometimes a glider cannot generate enough speed to get the desired amount of lift to climb to certain heights. When this occurs, one must employ two other forms of lift called thermal lift and ridge lift.
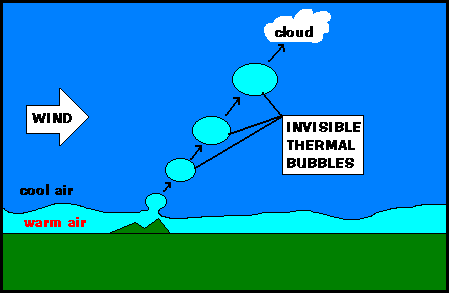
Thermal lift occurs when the sun heats the air just above the ground. This air then becomes warmer than the air around it and rises up in columns. When a glider hits one of these columns of air, it lifts them higher. Here is an illustration of this effect:

The lift force can be calculated by this equation: L = 1/2CLþAv2, where L is the lift force, CL is the coefficient of lift (which varies according to the shape of the wing), þ is the greek letter rho meaning air density, A is the cross-sectional area of the glider, and v is the velocity of the glider. This is very similar to the equation for drag, which is discussed in the next page. You can that the lift force is proportional to the square of the velocity. Now this is important because sometimes a glider cannot generate enough speed to get the desired amount of lift to climb to certain heights. When this occurs, one must employ two other forms of lift called thermal lift and ridge lift.
Thermal lift occurs when the sun heats the air just above the ground. This air then becomes warmer than the air around it and rises up in columns. When a glider hits one of these columns of air, it lifts them higher. Here is an illustration of this effect:

Image courtesy of: The
Physics of: Hang Gliding/ Paragliding
Ridge lift is another form of lift which occurs above
cliffs and large hills or mountains. When wind blows into the cliff
or mountain, it is forced up and over and creates a column of wind known
as an updraft. This type of lift is normally found in places where the wind
blows constant and hard, such as off of the ocean. Here is an illustration:
