
Static and Kinetic Friction
Friction is a key concept when you are attempting to understand car accidents. The force of friction is a force that resists motion when two objects are in contact. If you look at the surfaces of all objects, there are tiny bumps and ridges. Those microscopic peaks and valleys catch on one another when two objects are moving past each other.

This explanation is a little simplified. There are other processes at work, including chemical bonding and electrical interactions.
The level of friction that different materials exhibit is measured by the coefficient of friction. The formula is µ = f / N, where µ is the coefficient of friction, f is the amount of force that resists motion, and N is the normal force. Normal force is the force at which one surface is being pushed into another. If a rock that weighs 50 newtons is lying on the ground, then the normal force is that 50 newtons of force. The higher µ is, the more force resists motion if two objects are sliding past each other.
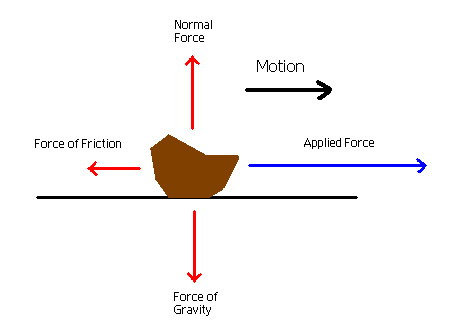
There are two forms of friction, kinetic and static. If you try to slide two objects past each other, a small amount of force will result in no motion. The force of friction is greater than the applied force. This is static friction. If you apply a little more force, the object "breaks free" and slides, although you still need to apply force to keep the object sliding. This is kinetic friction. You do not need to apply quite as much force to keep the object sliding as you needed to originally break free of static friction.
Some common values of coefficients of kinetic and static friction:
| Surfaces |
µ (static)
|
µ (kinetic)
|
| Steel on steel |
0.74
|
0.57
|
| Glass on glass |
0.94
|
0.40
|
| Metal on Metal (lubricated) |
0.15
|
0.06
|
| Ice on ice |
0.10
|
0.03
|
| Teflon on Teflon |
0.04
|
0.04
|
| Tire on concrete |
1.00
|
0.80
|
| Tire on wet road |
0.60
|
0.40
|
| Tire on snow |
0.30
|
0.20
|
These values are approximate.
Now, finally, how does all this relate to automobiles?
In some places, especially Alaska in the winter, you must keep friction in your mind constantly as you drive, in order to avoid an accident. You have to limit your speed in order to be able to stop at a reasonable distance, and to negotiate curves.
Braking distance can be calculated using the equation d = V^2 / 2gµ
Where:
d = Braking Distance
g = Acceleration due to gravity (9.80 m/sec^2)
V = Initial vehicle speed (m/sec)
µ = Coefficient of friction between the tires and the roadway
Notice that initial velocity is squared; this means that if you travel twice as fast, your stopping distance is squared, not doubled. This is why the two second rule ("travel at a speed so that two seconds pass between the moment the car in front of you passes a landmark and the moment you pass the same landmark") is not valid for high speeds; your stopping distance increases exponentially as you go faster.
A higher coefficient of friction decreases your stopping distance. It is better, therefore, for your tire to be using static friction rather than kinetic friction. If the tire is rolling along so that the surface touching the ground is never sliding, then static friction is acting to slow the car. If the wheels are locked and sliding, then kinetic friction is acting to slow the car. In order to utilize static friction when you need to stop quickly, there are several options. You can attempt to apply just enough brake to stay within the static range of friction and not too much to lock the tires. This is the best option, in terms of stopping you the quickest, but it can be difficult to be that precise with the brake. It can be especially difficult if you are about to hit a moose. Another option is pumping the brake, which has the effect of alternating the use of kinetic and static friction as the wheels lock and unlock. This is not quite as efficient, but easier to do in an emergency. A final option is to have your car take care of the braking for you, through antilock brakes or more sophisticated computer-controlled means. Antilock brakes do the same thing as you do; pump the brakes. The best solution is, of course, to drive slower.
Traveling around a curve causes you to experience a slightly different set of forces, as you must deal with the tendency for a car to want to travel straight ahead. This is explained by Newton's 1st law: an object will not change velocity without a force acting on it. In this case, you are causing the car to change lateral velocity and move to the side by applying frictional force from the tires. If the tires don't have a coefficient of friction large enough to provide the force needed to move the car laterally, then you slide straight forward and off the road.
Usually, the tires must maintain static friction in order to turn the car. That limits the maximum speed to a rate at which the tires do not slip. The equation that models this situation is:
Vmax = square root of (µ(static) g r)
Where:
Vmax = Maximum velocity
g = Acceleration due to gravity (9.80 m/sec^2)
r = Radius of curve
µ = Coefficient of static friction
If you are traveling around a curve with a radius of 10 meters and no snow or rain, Vmax = square root of (1.00 * 9.80 m/sec^2 * 10.0m) = 5.4 m/sec, which is about 22.1 mph. Any faster and the tires would slide.
If you are traveling around a curve with a radius of 10 meters on a snowy day, Vmax = square root of (0.30 * 9.80 m/sec^2 * 10.0m) = 5.4 m/sec, which is about 12.1 mph.