Free Bodies

If you were to take away the beer bellied bikers, and the smell of french fries this is what you would have. The free body diagrams should look like this:

       
     
 

The forces acting on this car, are the force of gravity (mgcos(O) & mgsin(O)), normal force, and the reaction force of tires acting against gravity.

 
     
             

The way torque is translated from the motor to the tires is illustrated below:
   
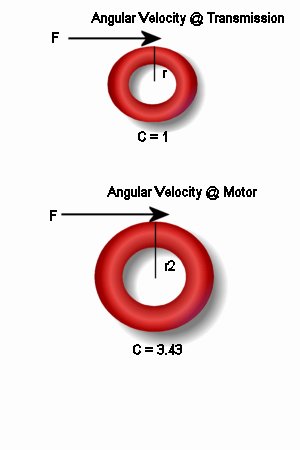
If a force is applied to two disks of enequal size, the torque is proportianal to increase in circumferance. The picture to the right illustrates this. Gear ratios can be compared to rolling discs. Two rolling discs with an angular velocity of of 3.34[rev/sec] and 1[rev/sec] respectively will travel the same distance if the circumferance of the slower one is 3.34 times that of the faster one. The faster moving disc can be thought of as the input into the gear, and the slower moving disc can be thought of as the output. The torque of the output will be proportianal to the angular velocity of the input..    

From Circumference to Torque:

r = 2 * 1 * (pi) r2 = 2 * 3.43 * (pi)

torque = t = 2F C* (pi)

=> (t1) = 2F*3.43*(pi) & (t2) = 2F*1*(pi)

[(t1)/2F * 3.43* (pi)] = [(t2)/2F*3.43*1)

(t1) = (t2)*3.43

generally, tf = ti * (gear ratio or omega)

t1 is directly proportional to t2 by the gear ratio.

  
       

There are a total of two gear reductions. One at the transmission (3.34:1) and one at the differential (3.73:1). If we multiply the two together we get the total ratio of 12.5:1 from the moter to the tires. This means for every one time the tires turn, the motor turns 12.5 times.

Using the equation to the right we can calculate the max resistive torque at the wheel caused by the motor.

(torque @ motor)*gear ratio = torque at tires

38*12.5 = 450ft*lbs