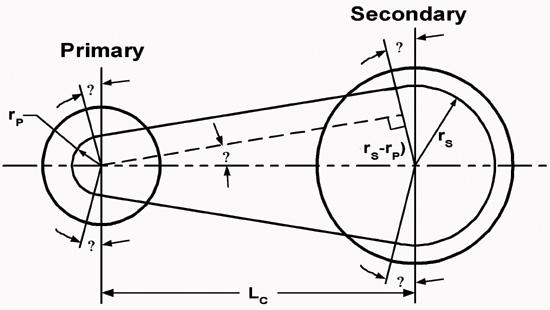
Diagram taken from SnowTech Magazine, available online at:
http://www.snowtech.com/
- First I'll address this notion of centrifugal force. In short, there is no such force. The object is merely experiencing radial acceleration, which you can think about as changing direction.
- Clutches, in effect, are really just variable diameter pulleys. The same equations work on pulleys as on clutches. For example, the speed of the belt can be found by taking the rpm of the primary pulley (or radial velocity) and multiplying it by 2(pi)r p, with rp being the radius of the belt that is going around the primary. This distance is labeled in the above diagram.
- Now that the belt speed has been found, the rpm of the secondary can be found by dividing the belt speed by 2(pi)r s.
- Torque multiplication can also be figured out. Torque equals force times the perpendicular distance from the line of action of the force to the access of rotation (rp or rs).
- If we are given that the engine puts out a torque of 100 ft-lbs and that rp = 2 in = 0.17 ft and r s = 6 in = 0.5 ft (now those are some good units!), we can find the force with which the primary pulls on the belt, and thus is transferred to the secondary. Force = torque / distance. Distance = rp . F = (100ft-lbs/0.17ft) = 588lbs. Now take the force and multiply it by 0.5ft to get T = 294ft-lbs. That's a torque multiplication factor of about 3! This calculation could also have been done easier by dividing r s by rp. This example is just slightly above "low gear." Most clutches range from about 4:1 to 1:1 ratios.
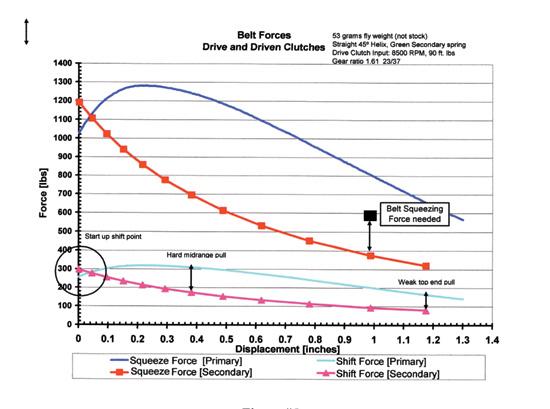
This graph was taken from SnowTech magazine, available online at http://www.snowtech.com/
- My next discussion is of the frictional forces between the belt and the sheaves of the clutches.
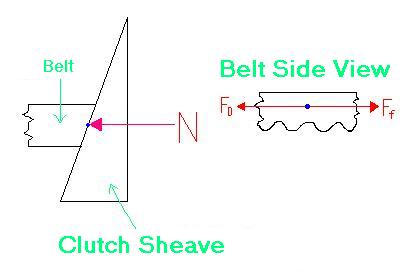
- I could not find a given value for the static coefficient of friction between rubber and aluminum (or any metal for that matter). The closest I could find (from several sources) was that between rubber and concrete which has a µs = 1.0 . I doubt that the coefficient is that high; I would guess more around 0.8 to 0.9.
- The frictional force can then be found given the normal force provided by the squeezing action of the clutch sheaves. The top two curves on the graph above shows the forces on the clutches throughout the full range of motion of the clutches.
- The maximum frictional force (F f ) = (µ s)(N) = (0.8)(1300 lb) = 1040 lb. This is more friction than is required to put the 588 lbs of force (F D , calculated in the above calculation of torque multiplication) into the belt without slipping (on the primary clutch). The secondary could still slip in this example, but it depends on how much torque is required to turn the track.

Image taken from http://www.snowest.com/
Well, that's all folks, hope you enjoyed it.
The only page left is the bibliography . If you somehow got here without going to the
home page first, please visit that too.
The only page left is the bibliography . If you somehow got here without going to the
home page first, please visit that too.