How Do Hydraulics Work?
To understand how hydraulics work, one must understand Pascal's Law.
Pascal's Law as stated in "Physics for Scientists and Engineers" is as follows:
A change in the pressure applied to a fluid is transmitted undiminished to every point of the fluid and to the walls of the container.
This means that if a fluid has pressure applied in one spot, the rest of the fluid undergoes the same pressure. The container of the fluid also undergoes the same pressure that is applied to the fluid. This only works for fluids that are incompressible like water or brake fluid. Air, on the other hand, is a fluid and is compressible. So not all fluids can be used for hydraulic fluid.
BACK HOME NEXT


http://www.familycar.com/brakes.htm
http://www.poclain-hydraulics.com/
main/english/technology/overview.htm
The white arrows, in the brake system picture, show how the pressure applied by the pedal is actually applying pressure to the entire system.
Another very important concept of Pascal's Law is that the pressure of a system is equal to the force divided by the area to which it is applied. P = F/A. Where P is pressure, F is the force, and A is the area.
Also, if there is a system with more than one cylinder, then the pressure of the input cylinder is equal to the pressure of the output cylinder. Pi = Po.
Therefore, Fi/Ai = Fo/Ao. The following diagram illustrates this principle.
Diagram from: http://home.earthlink.net/~dmocarski/chapters/chapter7/graphics/hydrolcs.gif
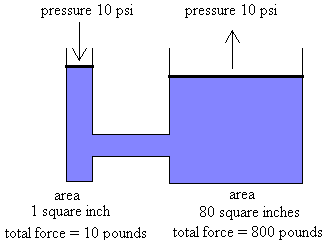
Pi = Po Fi /Ai = Fo/Ao 10 pounds / 1 inch = 800 pounds / 80 inches
The distance that each cylinder moves, is proportional to the volume displaced by the input cylinder.
So if the input cylinder with area (A) and moves a distance (Y), then: V = AY. For an two cylinder system: AiYi = AoYo => Ai/Ao = Yo/Yi
For the example above, if the left cylinder moved down 4 inches, the volume would be 4 cubic inches, (1x4). Therefore, the distance of the cylinder on the right would be 4/80ths, or 1/20th of an inch. AiYi/Ao = Yo => (1x4)/80 = 1/80
So, assuming energy is conserved (no losses in energy due to friction or other forces), the total work into the system is equal to the total work out of the system. Work = Force x Distance. W = FY Wi = Wo => FiYi = FoYo
Hydraulics that are used in today's machines are much more complicated than what was described above. Most use compressed air for the input force to be able to move the piston the necessary distance required to have a large distance on the output cylinder. As shown in the brake system diagram, the foot pedal is a lever that when pressed, increases the force applied to the input piston. These are just simple devices that make hydraulics an everyday tool. There are many more complicated devices that need not be explained for the simple understanding of hydraulics.