Diagram 1- Before Collision
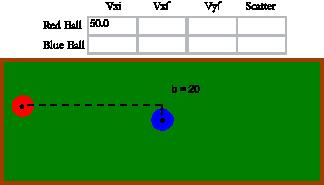
Drawn by Craig Caissie
Diagram 2- After Collision
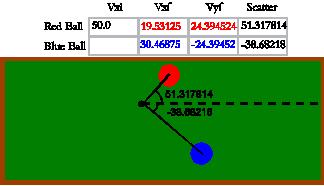
-Basic Momentum & Kinetic Energy
For the purpose of billiards we will not go into great detail as to what momentum
is. Basically though it can be thought of using the following equation;
p = mv
where p = momentum
m = mass of object
v = velocity of object
Kinetic energy is energy associated with the motion of an object. For basic purposes
we can just look at the following equation which relates kinetic energy with mass
and velocity of an object.
K = ½mv2
where K = kinetic energy
When you strike another ball with the cue ball it is almost a perfect elastic collision.
An elastic collision is one in which total kinetic energy as well as total momentum
are conserved within the system. This can be shown by the two basic equations;
Conservation of Kinetic Energy: ½m1v1i2 + ½m2v2i2 = ½m1v1f2 + ½m2v2f2
Conservation of Momentum: m1v1i + m2v2i = m1v1f + m2v2f
where m = mass of object
v = velocity
Since the cue ball has virtually the same mass as the other balls and the velocity of
our second ball will always be zero, since we are striking a static ball with the cue
ball. In addition this is considered a two- dimensional collision. From this we know
that momentum is saved within the y component and within the x component.
Therefore in the case of pool we can rewrite these two equations as:
Conservation of Kinetic Energy: ½m1v1i2
= ½m1v1f2 + ½m2v2f2
Conservation of Momentum: m1v1i = m1v1f cosø+ m2v2f cosØ
0 = m1v1f sinø - m2v2f sinØ
In this last equation the minus sign comes from the fact after the collision
ball two
has a y component of velocity in the downward direction from the x-axis. This can
be seen in the following diagram.
Diagram 1- Before Collision
Drawn by Craig Caissie
Diagram 2- After Collision
Drawn by Craig Caissie
The above diagrams show the initial velocity (both x and y directions) of both balls
(Vxi &Vyi) as well as the final velocities (Vxf & Vyf). As we can see Vxi = Vxf (total
of red and blue balls) as well as Vyi = Vyf. As one last note, since pool tables are not
frictionless these equations are not exact due to a small loss of energy due to friction
but they are close enough that your game will improve if these ideas are taken into
account.