What is Gravity?
 
 

 
 
 
 
 
 
 
 
 

What causes a cat to fall from the earth if you throw it from the top of the empire state building?
 
 

                                      

Most people will answer "gravity".  But what is gravity?  Lots of people know the effects of gravity because it affects us every minuet of every day of our life. However few people can tell you what actually causes it.

People used to believe that the motion of earthbound bodies and of those in space were governed by different laws. It was a common belief that everything in the universe revolved around the earth.  Around 1665, the famous Physicist Isaac Newton concluded that the force that keeps the moon and all other heavenly bodies in orbit around each other, was the same force that makes our cat accelerate towards the ground.
  All bodies attract each other with a certain force.  This tendancy of bodies to be attracted to each other is called gravitation.  Even though that it may be hard to beleive, right now you are exerting a gravitational force on the planet Pluto, and it in turn is exerting a gravitational force on you. In fact as you are reading this page, I am exerting a gravitational force on you!! I hope you don't find me to forward.

Newton's law of gravitation is a force law that gives us the magnitude of a force between two bodies (particles).

Newton's Law of Gravitation:                F = GMm/ r²            (1)

Where:
F= gravitaional force
G= gravitational constant, 6.67E^-11 N*m^2/kg^2
M= mass of body 1
m= mass of body 2
r = distance between the 2 bodies

You may ask, "Why does it seem like the earth is just sitting there while the cat falls towards it?"  The reason for this is that the earth is extremly massive, while the cat is very small. So although the cat pulls up on the earth, the rate that the cat pulls the earth towards itself is only tiny number; while the cat is pulled to the earth at a much greater rate.

To understand this lets look at Newton's second law which states:               F=ma          (2)
Where:
F=Force
M=mass
a=acceleration.

To find the acceleration of the cat towards the earth we will say that F in equation (2) is equal to the gravitional force between the cat and the earth, and therefore "a" from equation (2) is the acceleration of the cat toward the earth due to gravity.
If we now set equation (2) equal to that of Newton's Law of Gravitation (1), we get:              a = GM/r²           (3)
Where:
a = gravitational acceleration
G = gravitational constant
M = the mass of the earth (for this example)
r = distance between the cat and the center of the earth

Since this equation does not have the mass variable in it from the object that is being attracted toward the center of the earth (ie. the mass of the cat), the acceleration is constant for all bodies that are near the surface of the earth no matter what their mass. The reason that they have to be near the surface of the earth is that, as you can see from equation (3), as the distance from the surface of the earth changes, so does your "r" value. And since "r" is in the denominator and is squared, as your distance from the surface of the earth increases, the gravitational acceleration becomes smaller.  Since most of what affects our every day lives happens near the earths surface, the gravitational acceleration of any body near the earths surface has been given a constant value of 9.8 m/s². There are factors, such as that the earth is not of uniform density and that it is rotating, that can cause the actuall value of the acceleration due to gravity to either increase or decrease.  These factors don't effect it by a great amount though.  Therefore, the value of 9.8m\s is the value given to gravitational acceleration near the earths surface.  This gravitaional acceleration constant is usually symbolized by the lower case letter "g".

So now we know that the cat accelerates toward the earth at 9.8 m/s^2.  However, since newton's law of gravitation (1) holds true the earth is being accelerated upward at a rate which is given by the equation                               a = Gm/r²            (4)
Where:
a = acceleration of the earth upward due to the cat
G = gravitational constant
m = mass of the cat (in this example)
r = distance between the center of the earth and the cat.

If you plug in reasonable values into this equation you will end up getting a very small number. Remember that the gravitational constant, G, is a very small number.  The mass of the cat is also relativly small. Therefore you are going to get a small number in the numerator.  The denominator however, is going to be a vary large number.  Therefore, the acceleration of the earth up toward the cat is going to be a very small number. So small that we certaintly can't detect any change. This is the answer to why the cat seems to fall toward the earth while the earth doesn't move up toward the cat. In fact, the earth is moving up toward the cat, but only a tiny amount.
 
 

As I stated earlier, we all know what the effects of gravity are intuitivly.  It is what gives us what we call our "weight" on the earth.  Often times people confuse weight with mass, when weight is actually a force.  Subing in W for the force in Newtons second law (2) we get:
                                                                                W=mg                (5)
where:
m = mass
g = acceleration of the body due to gravity, which is always 9.8m/s² near the surface of the earth

The reason why astronauts "weigh" less on the moon is that the acceleration due to gravity towards the center of the moon is much smaller than the acceleration due to gravitation towards the center of the earth.  This must be the case because cetainly there mass surely hasn't changed, so the only other factor that could change their weight would be the acceleration of the mass due to gravity.

Knowing the gravtitaional acceleration of a body near the earths surface also makes solving kinematic equations for those bodies much easier. Take the following problem for example:

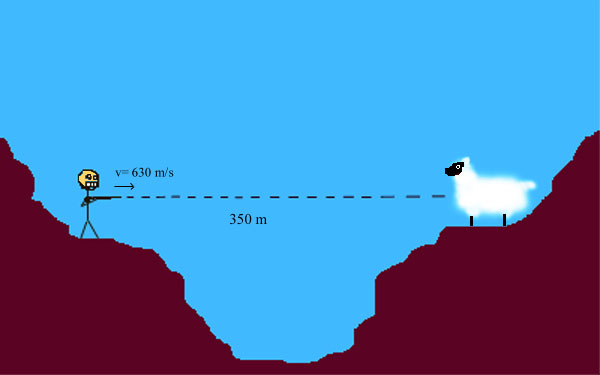
When hunting, it is important to realize that a bullet drops due to gravity. Lets say that you and Cletus the slack jawed yokel (thats for all you "Simpsons" fans out there) are in the mountains hunting for sheep. Cletus knows that his Ruger .243 has a muzzel velocity of 630m/s.  Suddenly of in the distance on the side of a mountain Cletus sees a sheep that is at roughly the same elevation as he is.  He pulls out his laser range finder and it tells him that the sheep is 350 meters away.  Not being the brightest when it comes to anything otherwise than performing the nescessary thought process to keep breathing, he tells you all this information and wants to know how high above the sheep he needs to aim.  Being English, you had better give your answer to Cletus in SI units.  The sheep looks skittish so he tells you to just forget about air resistance, he will take what ever estimation you give him.
How high above the sheep does he need to aim?
 
 

To solve this problem you will use the kinematic equations:

   x_f = x_i + V_ox(t) + 1\2(a)(t)^{2            (6)
and}
   y_f = y_i + V_oy(t) + 1\2(g)(t)²           (7)

The bullet will start from the chamber of Cletus's gun so we will give our y_i and x_i both a value of zero.
When the bullet leaves the gun, ignoring air resistance, there will be no acceleration in the x direction therefore the 1\2(a)(t)²  term in equation (6) drops out.

Since there is no initial velocity in the y direction the V_oy(t) term drops out of equation (7).

Now our equations look like:

x_f =  V_ox(t)             (8)

 y_f =  1\2(g)(t)²       (9)

To find the final y value, you will first need the time. You can get this from equation (8).

350 m = 630m/s(t)  = = = = = =>   t = 350m/630m/s = = = = = = =>  t = .56 sec

Now to find the distance that the bullet will drop, you put the value for the time into equation (9), using g = -9.8 m\s² because gravity is pulling in the negative y direction.

y_f = 1\2(-9.8m\s² )(.56)²

y_f = -1.54 meters

Therefore you tell Cletus that he must shoot roughly 1.54 meters above where he actually wants the bullet to hit.
 

As you can see, it is a good thing that Cletus decided to take into consideration the effect that gravity would have on his shot. If he hadn't he would most likely have missed the animal all together.

References:

Fundementals of Physics (extended)5th edition Halliday, Resnick and Walker (Wiley)

 http://www.curtin.edu.au/curtin/dept/phys-sci/gravity/index2.htm  (this is another web page on gravity)