Paper Airfoil Aerodynamics2 - Principles of
Flight | |
|
I.
A. Next B. Back
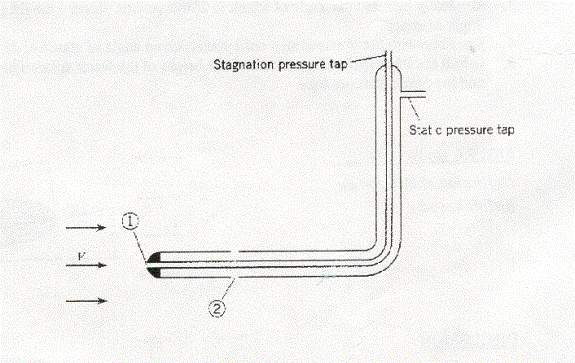
Daniel Bernoulli, a member of the Swiss family of mathematicians, studied the dynamics of fluid flow. He is honored today with a principle of fluid flow named after him: Bernoulli?s Principle. Bernouli?s principle shows that the average velocity of an ideal fluid is directly proportional to the pressure (A force over an area) it exerts upon a surface along that flow. Figure 1.1 shows an example of a device used to measure the velocity of moving fluids utilizing this principle. A pitot-tube utilizes the differences in pressures between the stagnant air at the tip and the moving air across the opening to determine the velocity. A greater difference in pressures means a greater fluid speed.
According to popular myth, Archimedes discovered the principles of
buoyancy while in his bath-tub.
As he found out, the pressure exerted upon a surface by a fluid is
directly related to its density.
A net balance of forces between the water displaced by the boat
(Higher density, and therefore higher pressure) and the space left behind
(Low density, and therefore low pressure) allows a boat to float upon the
water, even if the density of the material it is made of exceeds that of
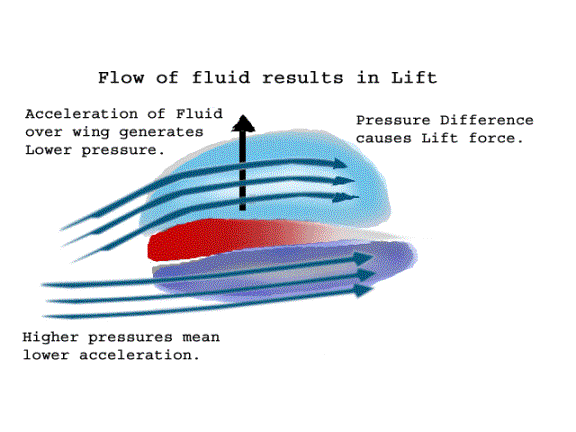
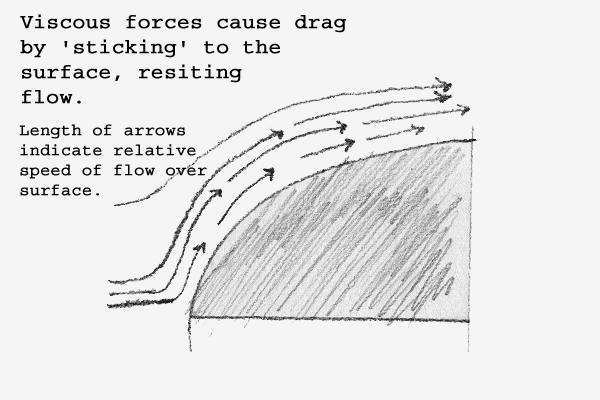
water. Lift is generated as fluid flowing across the top surface of the airfoil experiences an acceleration during its attempt to equalize the low pressure generated by the airfoil?s wake. This acceleration generates a region of lower pressure in the airflow above the wing, creating a lifting force. Unlike in a boat, the pressure forces do not cancel and so there is a net upward acceleration of the airfoil. Figure 2.2 illustrates this. As an object moves through a fluid, two forces combine to produce a resistance to that object?s motion. Viscous and Inertial drag forces are related through the fact that the resistance generated by moving through a fluid is directly related to an object?s Speed, it?s size (the cross sectional area and the planiform surface area of the object) the viscosity of the fluid, and the density of the fluid. This force is known as drag. Figure 2.3 shows how the inertial form of drag occurs. As the surface moves through the fluid, collisions between the surface and the particles of the fluid resist motion. This force is related to the density of the fluid, and the cross-sectional area of the surface in the average direction of the fluid flow. Figure 2.4 shows how the viscous form of drag occurs. As a fluid moves past a surface, a thin layer of fluid ?sticks? to the surface, resisting flow. This layer of fluid is referred to as the boundary layer. This resistance to flow is simply referred to as the viscosity of the fluid. The force exerted on the surface in opposition to the flow increases directly with the length the fluid must travel across the surface (Indirectly related to its surface area) Figure 2.5 displays a commercial viscosimeter used to measure the viscosity of a fluid based upon its resistance to motion. With this viscosity known, it is now possible to develop a relative measurement determining the amount of drag generated by an object as it moves through the fluid at various speeds. I.
A. Next B. Back |
Figure 2.1 ? A Pitot tube measures pressure differences between stagnant air (1) and moving air (2).
Figure 2.2 ? Pressure difference generates lift.
Figure 2.3 -- Inertial Drag Force
Figure 2.4 -- Viscous Drag Force
Figure 2.5 -- A commercial Viscosimeter |