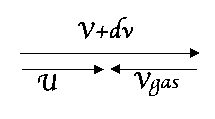The Physics Behind The Rocket

Rockets fly. We all know that. But how do they fly? And more importantly, how can we calculate how they will fly given certain parameters? The simple answer is that rockets fly by using Newtons third law, for every action there is an equal and opposite reaction. But the calculations that govern rocket motion are much more complicated than this. I will go over the derivation of these calculations here.

To figure out how a rocket will accelerate, we rely heavily on conservation of momentum. That is, for a given system, in our case the rocket-gas system, the TOTAL momentum will remain constant even if individual components move around. So if some component of the system (the gas) moves in one direction with a given momentum, some other object (the rocket) will have to move such that the two momentums exactly cancel each other out.

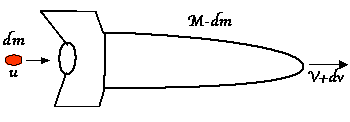
If a rocket is moving through space with a given velocity, V, it is quite easy to figure out its momentum, Pi, Since it is simply equal to the mass of the rocket times it's velocity.

Once you apply thrust, however, the situation becomes more complicated. You now have two masses to deal with, and two momentums to deal with. However, keep in mind that the total momentum of the system remains unchanged. So if we call the change in the velocity of the rocket dV, the mass of the gas emitted dM, and the velocity of the gas emitted relative to a stationary observer U, then the situation becomes Pf=U*dM+(M-dM)(V+dV), since the momentum of the system is equal to the momentum of the gas plus the new momentum of the rocket.

We now have all the elements we need to relate the velocity of the gas emitted to the velocity of the rocket, and to find the final momentum of the system. To do this, we will need to solve the above equation for the velocity of the gas. Our first step is to write U in terms of the velocity of the gas relative to the rocket and the velocity of the rocket. This relation ship can be modeled by the diagram below.

Writing this in equation form, we get U=V+dV-Vgas. Putting this into our original equation, we get

Pf=[s(V+dV)-Vgas]dm+(M-dM)(V+dV)

Since Pi=Pf, We can further rewrite the equation as

MV=[(V+dV)-Vgas]dm+(M-dM)(V+dV)

Mutiplying this equation out gives us

MV=VdM+dVdM-VgdM+MV+MdV-VdM-dMdV

Canceling Positives with negatives and canceling MV across the equal sign allows us to rewrite the equation as

0=-VgdM+MdV or VgdM=MdV

This equation is good for modeling the motion at a specific instant in time, but what if we were more interested in the change over a period of time, i.e. how much the rocket would accelerate if we applied thrust in the form of emitting gas at a certain velocity over a period of time? To modify the equation to model the situation over a period of time, we simply need to divide both sides by the change in time, or dt, which gives us the equation

Since dv/dt is acceleration, and mass times acceleration is force, we can further rewrite this equation as

Vg(dM/dt)=Ma=Fnt

where Fnt is the thrust provided by the gas. If we let R=dM/dt we can further simplify this equation to

Thrust=VgR

We can now use this equation to find the force produced by the rocket when given the mass of fuel burned, the original mass of the rocket, the distance covered during the burn, and the duration of the burn. Once we have that value, we can easily rearrange the equation to find other pieces of information, such as how long we would need to burn to change the speed of the rocket, dv, by a certain amount. See a sample calculation