Newton applied these three laws to Keplerís laws of orbit to come up with the law of universal gravitation. This gave us the reason why the moon doesnít fall out of the sky and hit the earth (web 2). This came about through a well-known story; it was on seeing an apple fall in his orchard that Newton conceived that the same force governed the motion of the Moon and the apple (web1). He calculated the force needed to hold the Moon in its orbit, as compared with the force pulling an object to the ground. Newton identified gravitation as the fundamental force controlling the motions of the celestial bodies. He never found its cause. To contemporaries who found the idea of attractions across empty space unintelligible, he conceded that they might prove to be caused by the impacts of unseen particles (web 1).

He thought out the fundamental principles of his theory of gravitation, namely, that every particle of matter attracts every other particle, and he suspected that the attraction varied as the product of their masses and inversely as the square of the distance between them (web 5). Leaving out the details and only taking round numbers, his reasoning at this time on the theory of gravitation seems to have been as follows. He suspected that the force, which retained the moon in its orbit about the earth, was the same as terrestrial gravity ( web 4). He knew that, if a stone were allowed to fall near the surface of the earth, the attraction of the earth caused it to fall 9.8 meters per second. The moon's orbit relative to the earth is nearly a circle, taking it to be so, he knew the distance of the moon, and therefore the length of its path; he also knew that the time it took the moon to go around the earth once was a month.

(Web4)

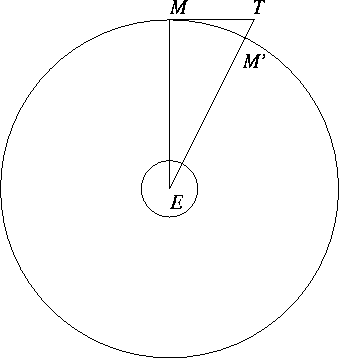
From this he could easily find its velocity at any point such as M on figure 3. He could from there find the distance MT through which it would move in the next second if it were not pulled by the earth's attraction. At the end of that second it was however at M', and from that the earth E must have pulled it a distance TM' in one second (assuming the direction of the earth's pull to be constant). Now he and several physicists of the time had conjectured from Kepler's third law that the attraction of the earth on a body would be found to decrease as the body was moved farther away from the earth and inversely from the center of the earth. If this were the actual law, and if gravity were the sole force which retained the moon in its orbit, then TM' should be 9.8 meters per second inversely as the square of the distance of the moon from the center of the earth to the square of the radius of the earth. Later when Newton repeated the investigation, TM' was found to have the value which was required by the hypothesis, and the verification was complete; but in 1666 his estimate of the distance of the moon was inaccurate, and when he made the calculation he found that TM' was about one-eighth less than it ought to have been on his hypothesis (web 4). This didnít however discourage his faith in the belief that gravity extended as far as the moon and varied inversely as the square of the distance. It seems, moreover, that Newton already believed firmly in the principle of universal gravitation, that is, that every particle of matter attracts every other particle, and suspected that the attraction varied as the product of their masses and inversely as the square of the distance between them (web 4).

And that was just some of the major parts that Newton gave future physicist to think about. He was very helpful in this department and if it wasnít for his conjectures it might have set back physics decades before someone else ever came accost it again and proved it as he did.