Perhaps the most dramatic progress in understanding minerals came with the discovery of X-rays. In 1912 German physicist Max von Lane (1879-1960) demonstrated that crystals would diffract X-rays, thus providing that minerals posses a regular and repeating internal arrangement of atoms. By 1914, W.H. Bragg (1862-1942) and his son W.L. Bragg (1890-1971) in Cambridge, England had used X-rays to determine the structure of minerals. The equation they derived in doing so has now become known as Bragg’s Law:

nl = 2d sin q, for n = 1,2,3…

Where n is a positive integer (the index), l is the wavelength, d is the distance between layers of atoms in the crystal, and q is the angle from the crystal plane (not the usual normal). The Braggs were awarded the Nobel Prize in physics in 1915 for their work in determining crystal structures beginning with NaCl, ZnS and diamond. Although Bragg's law was used to explain the interference pattern of X-rays scattered by crystals, diffraction has been developed to study the structure of all states of matter with any beam, e.g., ions, electrons, neutrons, and protons, with a wavelength similar to the distance between the atomic or molecular structures of interest.

Back to top

The wavelength of X-rays used in X-ray diffractometers is around 1 or 2 Å (10^-10m), which is similar to the spacing of atoms in the structure of most minerals. The similarity in dimensions means that the regularly spaced atoms that comprise a crystal diffract X-rays. Based on the analysis of this diffraction in three dimensions, it can be shown that the layers of atoms produce diffraction maxima that effectively "reflect" the incident X-rays if the angle of incidence q is appropriate.

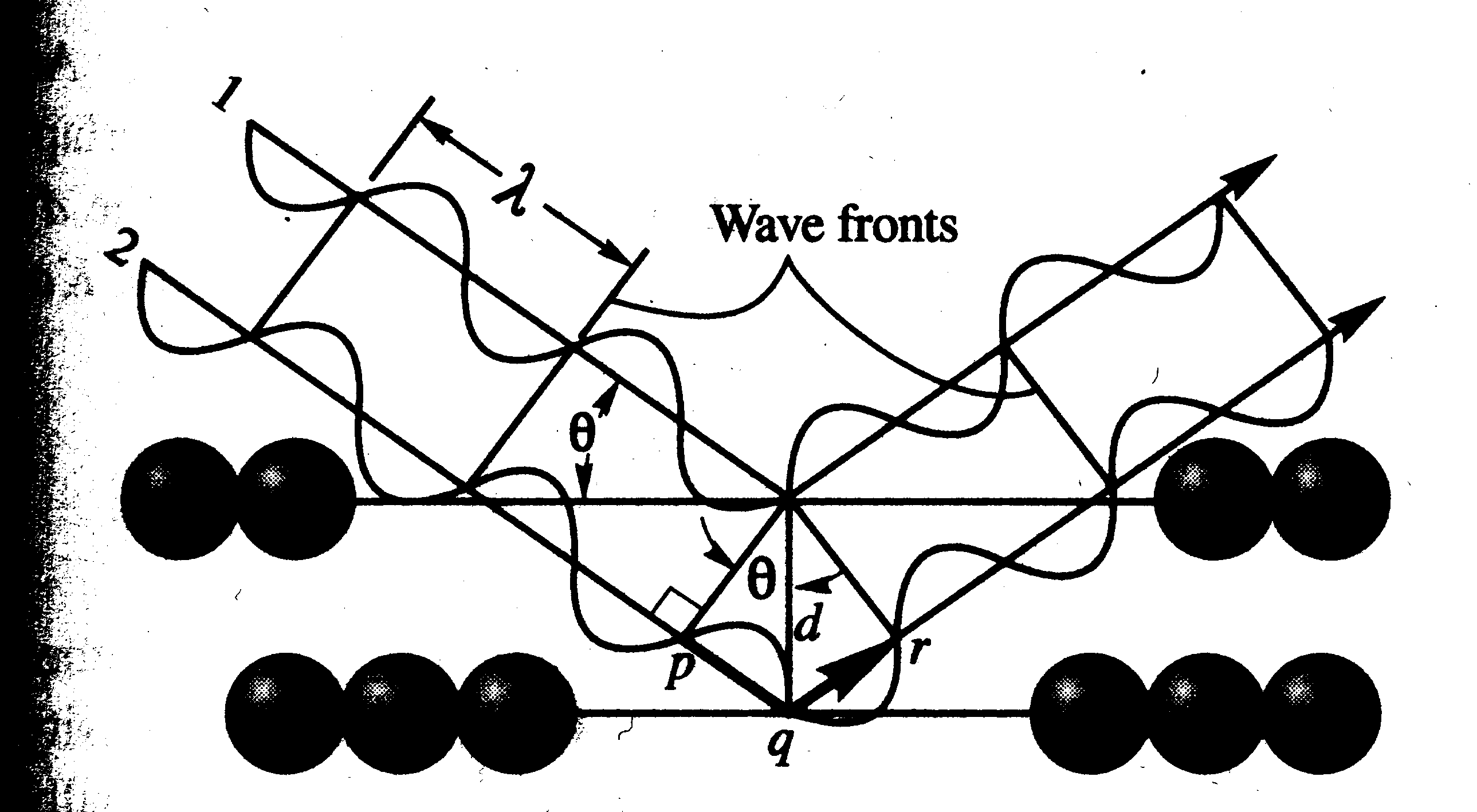
Rays 1 and 2 are incident to the layers of atoms at angle q. The planes of atoms are spaced distance d apart. Diffracted X-rays from each plane of atoms will be in phase only if the angle q is such that the additional distance pqr traveled by wave 2 is equal to an integer number of wavelengths

pqr = nl (Equation 1)

Where n is an integer and l is the wavelength of the X-rays. The distance pqr is twice the distance pq, which is related to the interplaner spacing d by the equation

pq = d sin q (Equation 2)

or

pqr = 2pq = 2d sin q (Equation 3)

Combining Equations 1 and 3 yields

nl = 2d sin q (Bragg’s Law)

Back to top

In a single crystal setup, an X-ray detector is mounted as shown in this figure. A mechanical device keeps the detector oriented so that the angle of incidence equals the angle q of reflection for the desired crystal plane. Peaks in the X-ray detection rate are sought as the angle is varied. The advantage of this type of apparatus is that diffraction peaks from only the selected crystal plane are observed.

Back to top

The powder in a powder target is really a conglomeration of many tiny crystals randomly oriented. Thus, for each possible Bragg diffraction angle there are crystals oriented correctly for Bragg diffraction to take place. The detector is usually a photographic plate or an equivalent electronic device. For each Bragg diffraction angle one sees a ring on the plate concentric with the axis of the incident X-ray beam. The advantage of this type of system is that no a priori knowledge is needed of the crystal plane orientations. Furthermore, a single large crystal is not required. However, all possible Bragg scattering angles are seen at once, which can lead to confusion in the interpretation of the results.

Back to top

The following figures show experimental x-ray diffraction patterns of cubic SiC using synchrotron radiation.

Back to top

Back to top

Last revised: 11/22/00